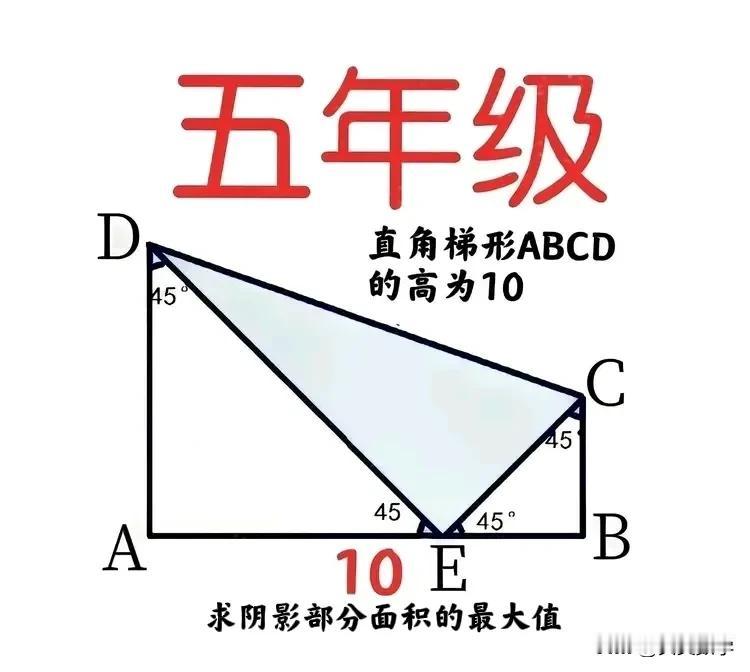
“难度超大,极具挑战性!”限用小学知识,不少家长朋友也不会!小学五年级数学竞赛题:十分考验孩子的化归能力和几何直观能力! 如图,E为直角梯形ABCD的高AB上一点,AB=10,ADE和BCE均为等腰直角三角形,求阴影部分三角形CDE面积。 解题关键:AD+BC=AB ——————————— 提示一:拼图+化归!适合五年级 ①AD=AE,BC=BE,故AD+BC=AB=10, ②用两个相同的梯形拼成一个边长为10的正方形,中间阴影部分为一个长方形。 ③化归:一个边长为10的正方形“切掉”角上4个等腰直角三角形,求剩余部分阴影长方形面积的最大值。 ④当阴影长方形为正方形时,面积最大,此时4个角上的等腰直角三角形的直角边均为5,从而S阴影长方形=100-4×5×5÷2=50,故阴影三角形CDE面积最大值为50÷2=25。 提示二:重要不等式!适合高中生 ①令AE=a,BE=b,则a+b=10,S梯形=50。 ②S△CDE=50-(a²+b²)/2≤50-(a/2+b/2)²,a=b时等号成立,故S△CDE≤50-25=25。 提示三:勾股定理+重要不等式!适合高中生 令AE=a,BE=b,则a+b=10,DE²=2a²,CE²=2b²,从而S△CDE=ab≤(a/2+b/2)²=25。 友友们,怎么看?欢迎留言分享!
评论列表