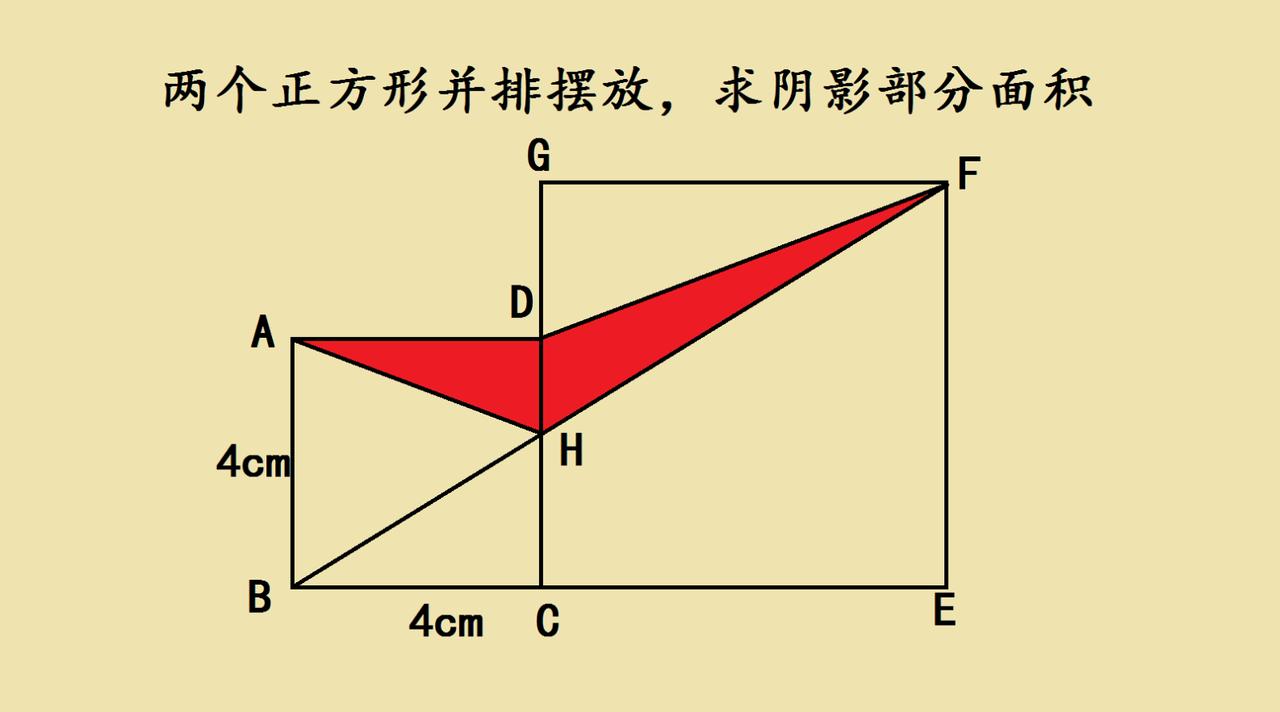
五六年级几何题:两个正方形里的阴影,原来可以这么“巧”算! 五六年级的几何题,有时候盯着图硬算反而绕远——比如这道两个正方形的阴影面积题,不用列算式,换个思路就能秒懂~ 其实不用死算三角形面积,试试“转化”:把分散的阴影部分,通过图形里的平行线、等底等高这些隐藏条件,把它们“拼”或者“移”到一起。你会发现,这些零散的红色区域,其实能凑成一个规则图形的面积~ 关键是别被复杂的线段绕晕,先观察图形里的“相等关系”——比如正方形边长一样长,三角形的底和高其实藏在正方形的边里。有时候换个角度看,难题就变成了“一眼题”~






评论列表