[LG]《Optimal Control Theoretic Neural Optimizer: From Backpropagation to Dynamic Programming》G Liu, T Chen, E A. Theodorou [Meta & Georgia Institute of

Technology & Apple] (2025)

本文提出了一种全新的深度神经网络（DNN）训练优化器——最优控制论神经优化器（OCNOpt），基于将DNN视作动态系统并借鉴最优控制编程（Optimal Control Programming, OCP）框架。核心贡献和洞见如下：

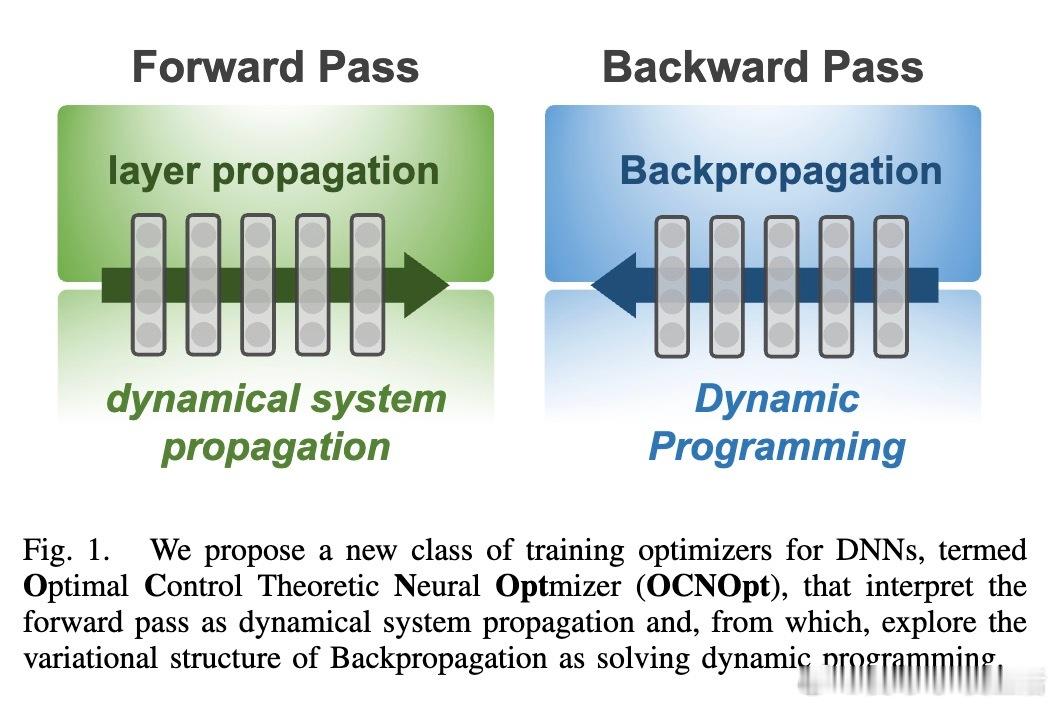
1. 从动态规划到反向传播的统一视角

传统的反向传播算法实质上是对动态规划中的Bellman方程进行一阶近似展开的过程，实现了梯度计算和参数更新。本文首次揭示了这一变分结构，将DNN训练视为动态系统优化问题。

2. 引入二阶信息的微分动态规划（DDP）算法

在此基础上，OCNOpt通过保留Bellman方程的二阶导数项，应用微分动态规划，获得了层级反馈控制策略，带来更丰富的算法设计空间，包括：

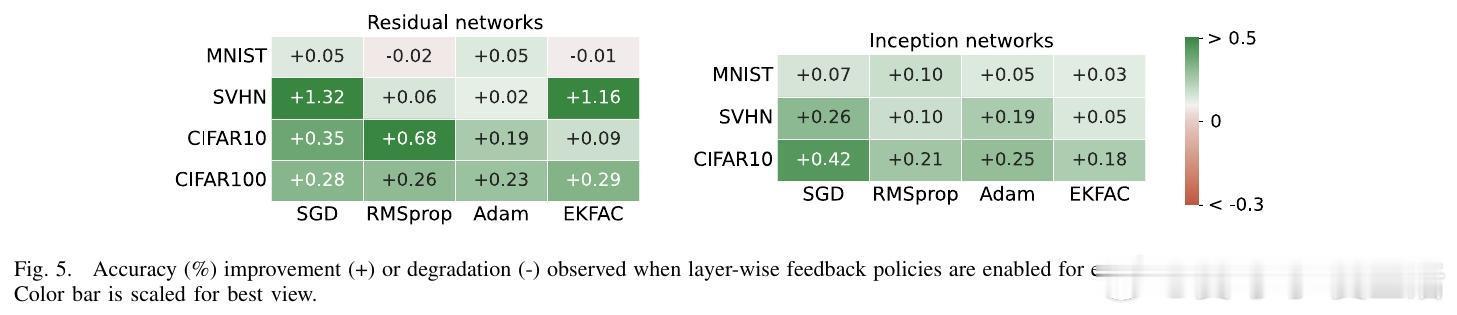
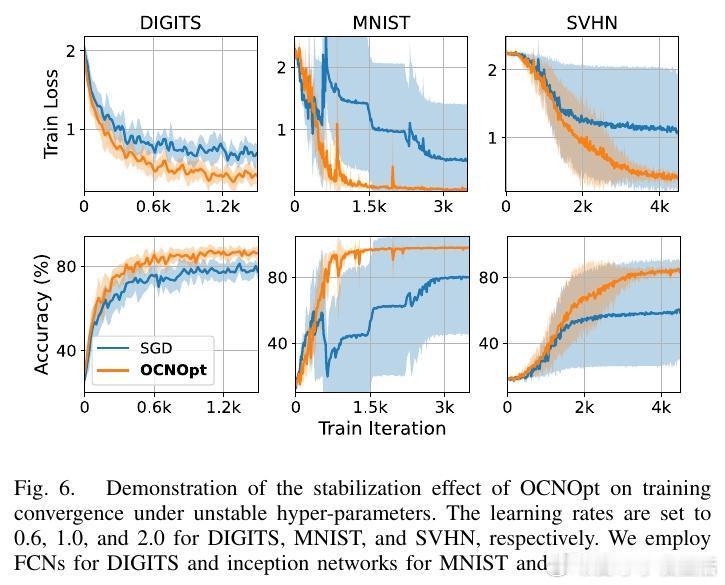
- 层级反馈增益，增强训练过程的鲁棒性和稳定性

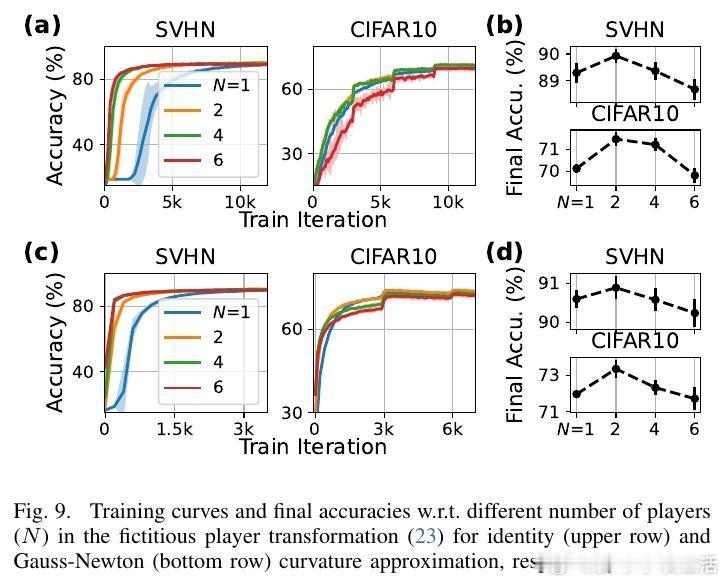
- 融入博弈论机制，支持多玩家协作或竞争的训练框架

- 适用于连续时间模型，如神经常微分方程（Neural ODEs）的高阶训练

3. 高效的低秩分解与曲率近似

针对二阶矩阵维度过高的计算难题，本文提出利用Gauss-Newton近似及Kronecker分解等技术，大幅降低计算复杂度，使得OCNOpt在保持二阶优化优势的同时，具备可扩展性和实用性。

4. 广泛适用的网络架构与任务

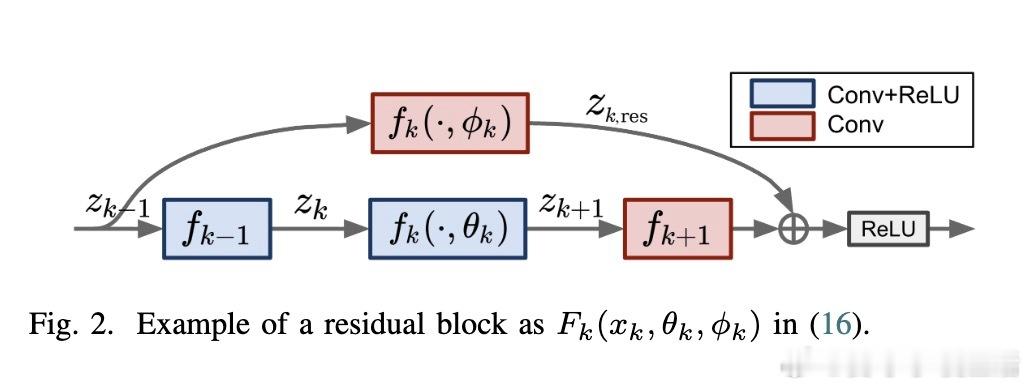
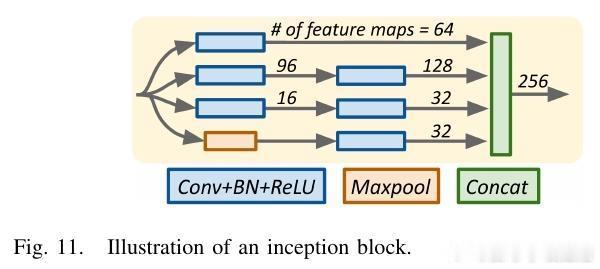
OCNOpt支持多种主流DNN架构，包括全连接网络、卷积神经网络、残差网络、Inception结构及Neural ODEs，涵盖图像分类、时间序列预测、概率建模等多样任务。

5. 实验验证优越性能

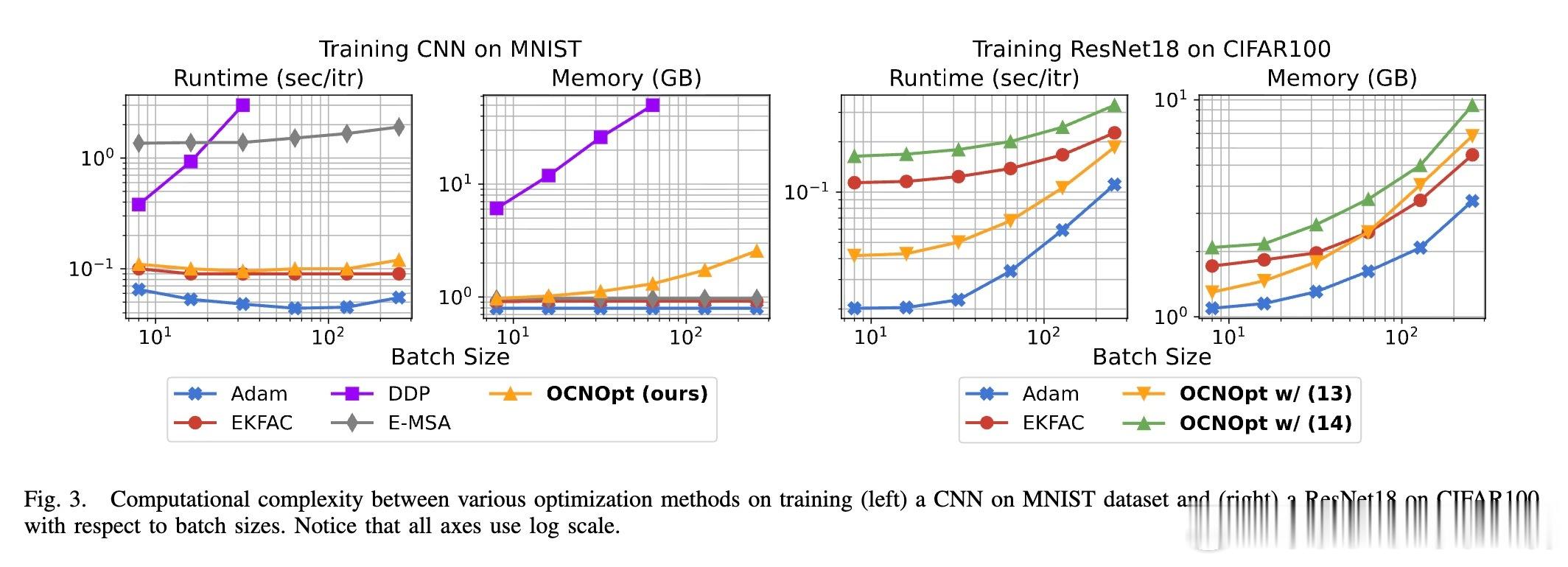
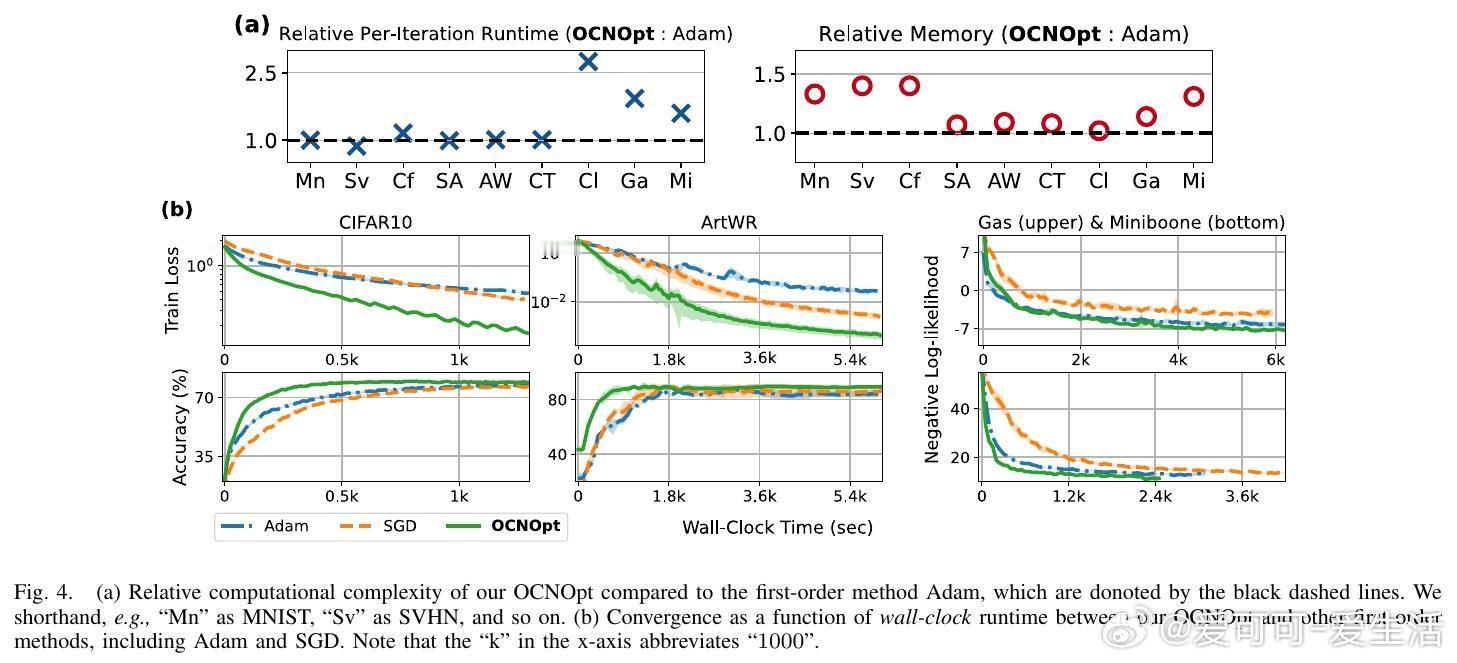
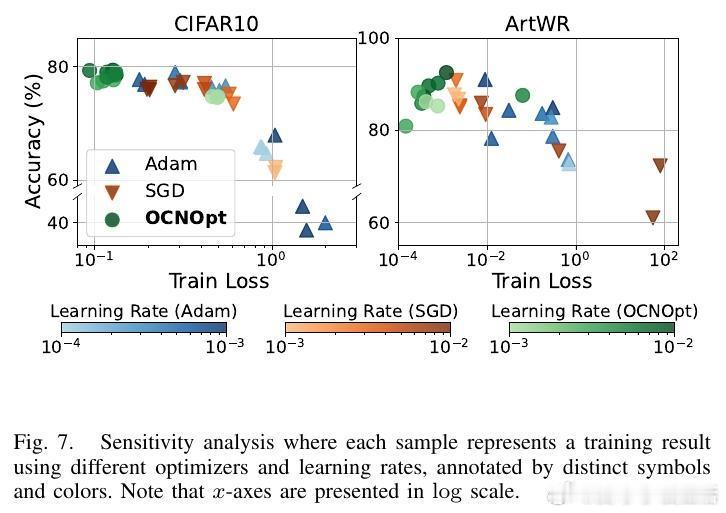
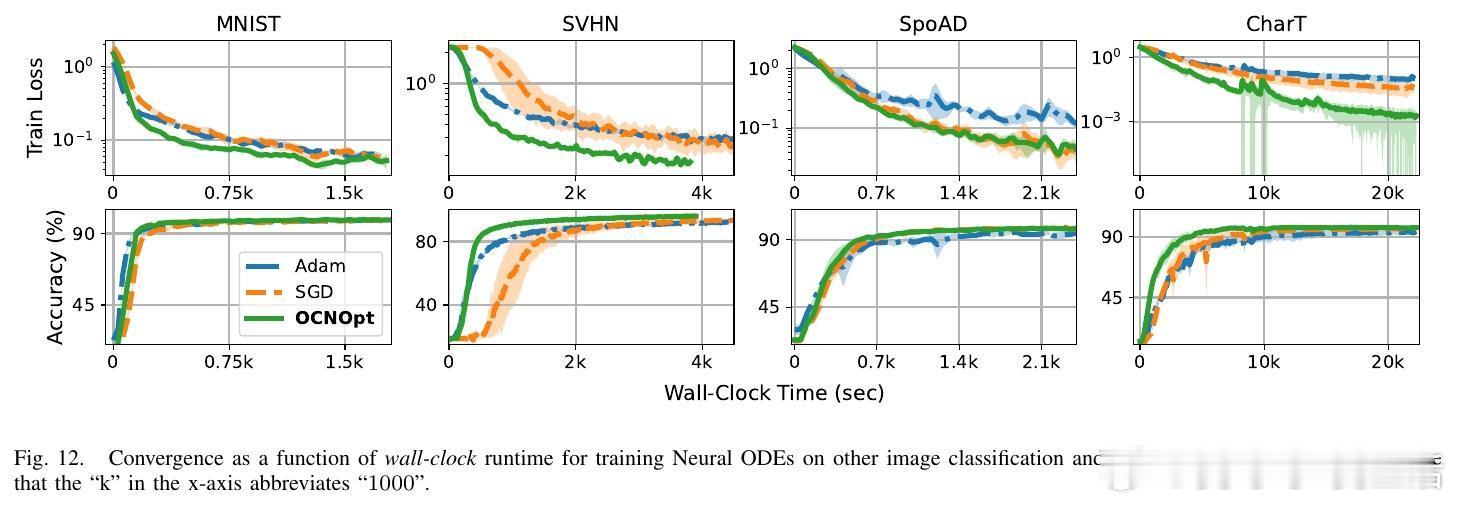
实验结果显示，OCNOpt在多个公开数据集（如MNIST、CIFAR10、SVHN等）和多种网络架构上，均优于传统一阶优化器（SGD、Adam、RMSProp）及现有OCP启发方法，表现出更快的收敛速度、更强的鲁棒性和更高的测试准确率，同时计算资源需求可控。

6. 算法创新与未来方向

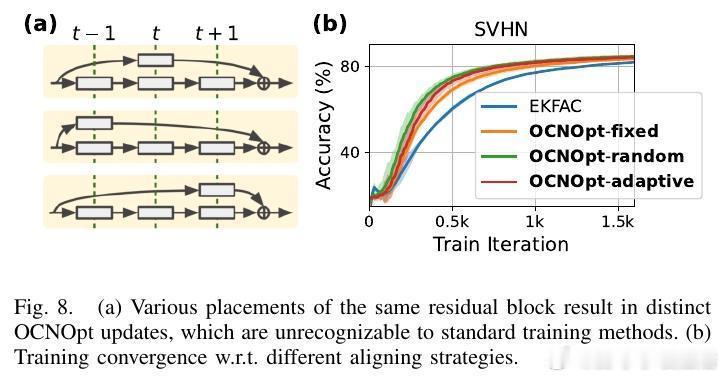
- 通过博弈论视角，提出动态层间对齐策略和多玩家合作框架，进一步提升训练效果

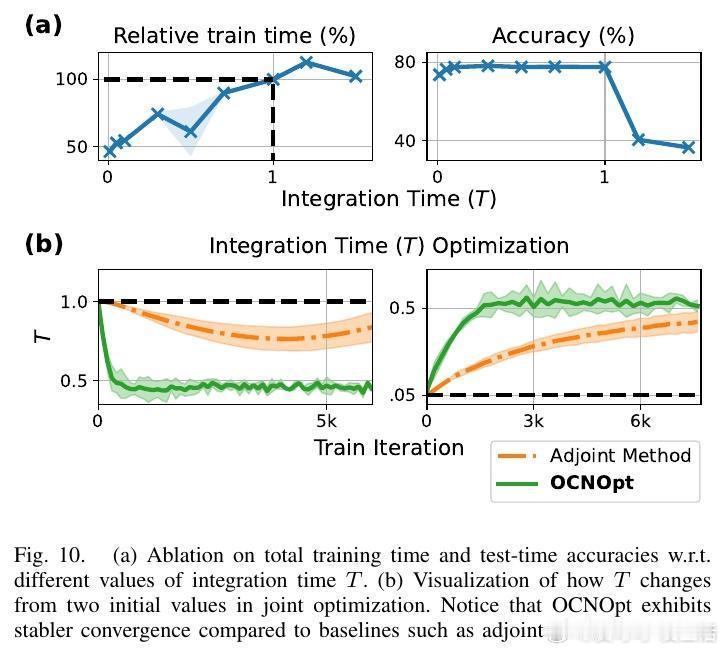
- 提出联合优化神经ODE积分时间的新思路，实现训练时间和性能的折中优化

- 展望将该理论推广至神经随机微分方程、偏微分方程和Transformer等前沿架构

总结而言，OCNOpt以最优控制理论为基石，融合现代深度学习训练需求，开辟了基于动态系统优化的神经网络训练新范式。它不仅理论上统一了反向传播和动态规划，更在实践中提供了性能和稳定性的显著提升，具备广泛的应用潜力和研究价值。

详细内容及算法实现请参见论文原文：arxiv.org/abs/2510.14168