城市中摩托车等微交通工具与汽车混行带来了严峻挑战，传统交通流理论难以刻画其复杂的非平衡动力学。瑞士洛桑联邦理工学院（EPFL）等团队基于大规模无人机数据，首次建立了机动性与速度的非线性关系。他们构建了一个非平衡多物种交通模型，揭示了从有序车道流到无序簇状流的相变过程，并证明其由一个普适性标度指数主导，为理解复杂交通现象提供了全新的物理学视角。

标题：Universality in multispecies urban traffic「多物种城市交通流中的普适性」

作者：Georg Anagnostopoulos, Nikolas Geroliminis

期刊：Communications Physics

理论创新：将非平衡物理中的有向逾渗（Directed Percolation, DP）理论引入城市异质交通流研究，为理解交通拥堵的形成机制提供了全新的普适性物理框架。

经验发现：基于大规模真实轨迹数据，首次识别并量化了微交通工具的机动性与其速度之间的非线性指数关系，并发现了城市交通中预期碰撞时间（TTC）的幂律分布，证明了其远离平衡态的本质。

模型构建：开发了一个新颖的、内在非平衡的智能体模型，该模型创新性地耦合了基于“样本空间规约”的动态转向行为和基于Newell非线性模型的随机跟驰行为。

现象揭示：通过仿真复现并揭示了城市异质交通系统中存在的非平衡相变：系统从有序的“车道流”状态转变为无序的“簇状拥堵”状态，其临界行为由DP普适类决定。

涉及摩托车在混合交通中，以及更广泛的自行车和城市中其他新型微出行工具的集体现象备受关注，因为这些弱势道路使用者的行为引发了重大的安全问题。当有限的城市基础设施与汽车等传统车辆共享时，情况尤其如此。然而，从物理学的角度来看，这个主题严重缺乏研究，并且城市异质交通尚不存在坚实的理论基础。通过研究pNEUMA数据集，我们首先建立了机动性与速度之间的非线性关系，这映射到样本空间规约过程（SSR）的非平衡概念。将SSR与Newell的非线性交通模型相结合，我们确定了平均机动性（解释为温度）与摩托车和汽车群体之间的平均速度差之间的幂律关系。仿真结果使我们能够从车道形成有序状态恢复到由一个普适缩放指数控制的簇形成无序状态的非平衡相变，该指数对交通条件和模型变体均具有鲁棒性。我们的贡献在微观行为和渗流的宏观理论之间建立了联系。

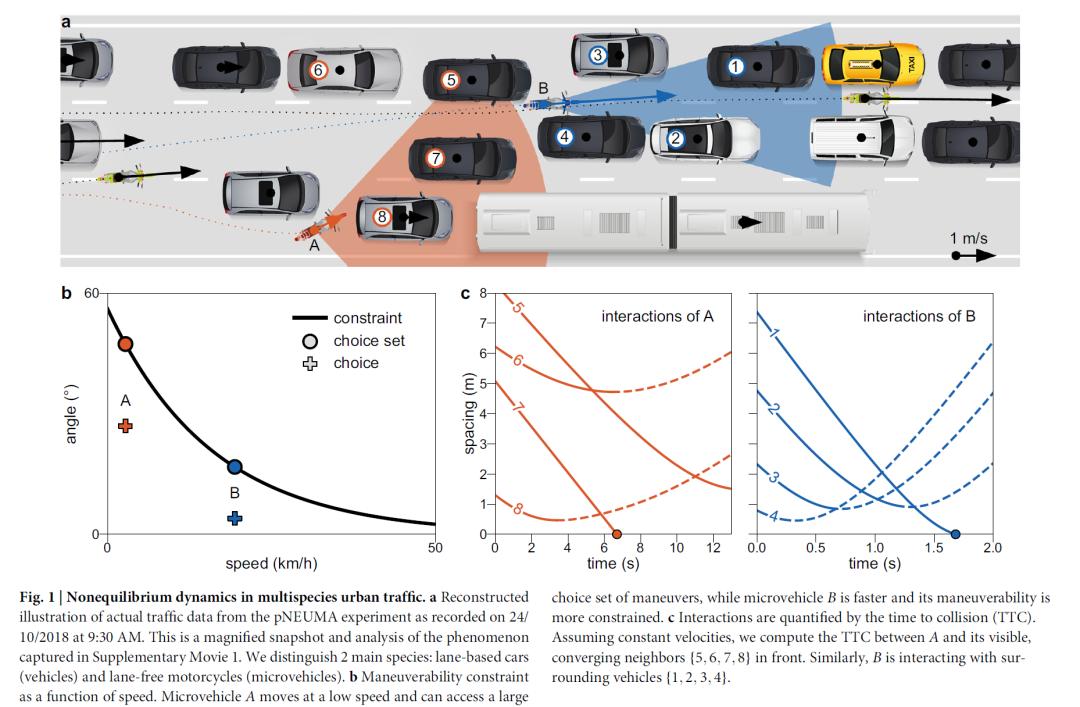
摩托车、电动自行车等微交通工具在城市中日益普及，它们与传统汽车共享有限的道路资源，形成了复杂的城市异质交通流。这种交通模式引发了严重的安全隐患，但从物理学角度对其进行的研究却严重不足，缺乏坚实的理论基础。

现有的交通流模型，如LWR模型及其扩展，大多基于强平衡假设，难以捕捉真实交通中远离平衡态的集体行为和临界现象。即使一些所谓的“非平衡”模型，也仅仅是增加了松弛项，并未触及系统的核心驱动机制。因此，学术界亟需一个能够描述城市异质交通系统内在非平衡特性的、更本质的理论框架。

本文以此为切入点，旨在摒弃传统的平衡态近似，转而从非平衡物理和复杂系统的视角出发，探究混合交通的基本物理机制。研究的目标是建立一个“模型的模型”，即一个能够揭示系统普适性（Universality）的简约框架，将微观的驾驶行为与宏观的物理理论（如逾渗理论）联系起来，从而更深刻地理解和预测混合交通的动态演化。

本文提出一个内在的非平衡多物种交通模型，通过智能体仿真来复现和研究摩托车（微交通工具）与汽车（常规车辆）的相互作用。模型的核心在于将两种关键的驾驶行为动力学进行耦合。

模型首先从PNEUMA数据集中发现，微交通工具的机动性（以最大可转向角度度量）与其速度之间存在一个非线性的指数衰减关系。这被抽象为一个“样本空间规约过程”（Sample Space Reducing, SSR），即速度越快，可供选择的转向操作空间越小。该关系通过分位数回归估计得出：

其中，和是经验估计参数。在每个决策时刻，微交通工具会在其动态变化的机动性约束下，选择一个能最大化“动态孔隙度”（dynamic porosity）的行驶方向，即朝向最开阔、碰撞风险最低的方向行驶。动态孔隙度定义为：

其中是期望速度，是在角度方向上的预期碰撞时间（TTC）。

车辆的纵向运动（跟驰行为）采用了Newell的非线性模型（NNM）。该模型将车辆间距映射到一个最优速度，其形式如下：

该模型包含三个核心参数：期望速度、间距以及间距处的速度梯度。模型同时考虑了异质性（每个驾驶员有不同的参数）和随机性，通过Ornstein-Uhlenbeck (OU) 随机过程来模拟驾驶行为中的扰动。最终，车辆的运动由一组耦合的随机微分方程描述，整合了转向、跟驰和随机噪声。

为了研究系统的宏观集体行为，作者引入了物理学中的概念。他们定义了系统的“温度”作为所有微交通工具机动性的平均值，以及一个序参数作为两类交通工具平均效率的差异。通过分析在不同交通密度下，序参数如何随温度变化，来识别系统是否存在相变及其临界特性。

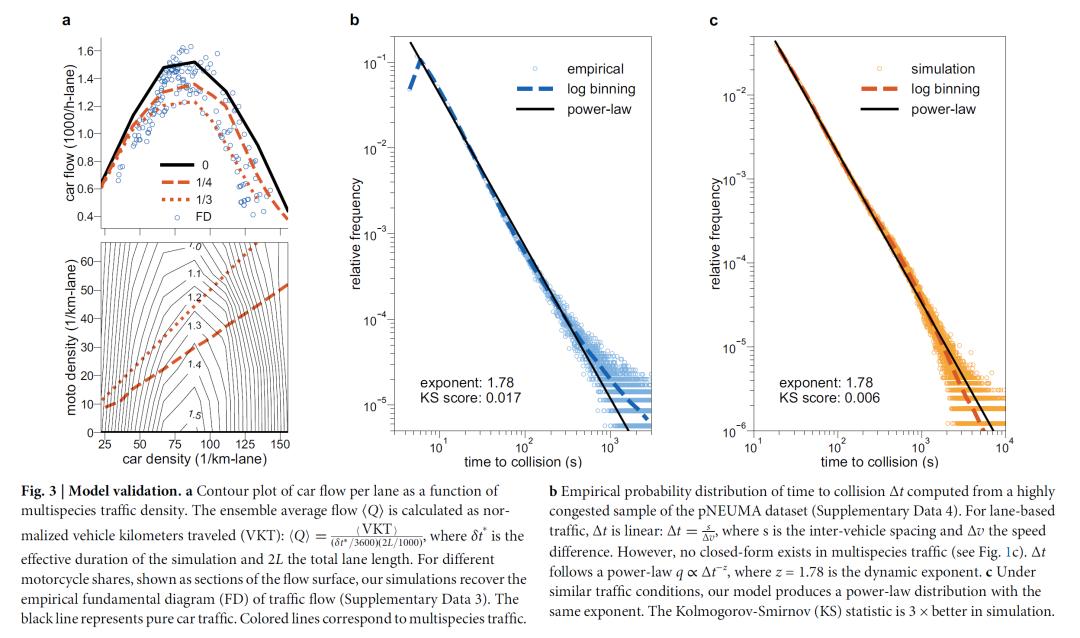
研究的核心结论在于从经验和理论两个层面揭示了城市异质交通的非平衡物理特性。

首先，研究首次在交通领域识别出一个重要的幂律分布。分析显示，无论是真实的PNEUMA数据集还是模型仿真数据，车辆的预期碰撞时间（Time-to-Collision, TTC）分布都遵循一个显著的幂律，且具有相同的幂指数。这一发现强有力地证明了城市交通系统是一个远离平衡态的系统，其稳态条件比传统理论预设的要罕见得多。

其次，本文最关键的发现是识别出一个非平衡相变及其普适性。研究表明，城市异质交通系统存在一个从有序的“车道形成”（lane formation）状态到无序的“簇形成”（cluster formation）状态的相变。这一相变由系统的平均机动性（被定义为“温度”）驱动。在临界点附近，系统的序参数与距临界温度的距离之间遵循幂律关系，其临界指数经数据拟合为。该指数与（1+1）维有向逾渗（Directed Percolation, DP）普遍性类的理论值高度吻合。这一结果表明，尽管交通模型细节复杂，其宏观临界行为却由一个普适的物理规律所支配，从而将微观的交通行为与宏观的逾渗理论深刻地联系起来。

尽管本研究取得了重要进展，但作者也指出了未来的研究方向：

需要进一步研究更优的控制参数和序参数来验证DP假设，并尝试通过将当前模型转化为时空格点模型来计算出DP全部的3个临界指数。

当前模型假设汽车没有横向动力学，未来需要放宽这一假设，将汽车的换道行为整合到模型中，因为换道是引发交通拥堵和不稳定的重要因素。

需要检验本文提出的普适性原理是否适用于其他类型的异质性人群，例如无车道划分的印度交通、行人与电动滑板车混合的交通，甚至是其他非人类的集群系统。