我们生存的宇宙空间是立体空间，我们所接触到的物体都占有空间的一部分。立体几何研究的就是现实世界中物体的形状、大小与位置关系，对于我们理解空间图形、掌握物体特征、运用特征解决实际问题具有重要的意义。学生在本单元要学习的内容包括空间几何体、平面的基本事实与推论、空间中的平行关系、空间中的垂直关系等部分。知识体系如下。

本期首先针对第一部分“空间几何体”介绍相应的学习方法，希望能够帮助同学们更好地掌握相关知识，提升你的数学素养。

01 空间几何体与斜二测画法的学习方法

空间几何体是一个抽象的概念，我们用“物体占有的空间形状和大小”来描述几何体。学生在生活中会接触非常多的几何体，如长方体形、柱形、球形等建筑或物品，以及常见几何体的组合，比如带屋檐的房子、倒置的棱台等。学生可以细心观察生活，学会从不同视角观察几何体，在脑海中积累几何体的各种特征，理解“斜二测直观图”，为后续的学习打下基础。

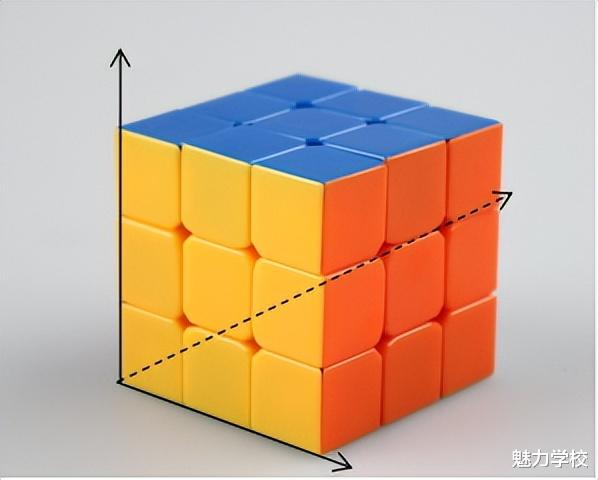
比如可以拿一个正方体（比如魔方），测量其边长，然后观察该正方体在“斜二测”视角下，即眼睛“与y轴成45°、高出xOy平面45°”的视角下，看着变成了什么样子，将看到的图形画在纸上，并测量画出来的各个边长与客观测量的边长有何异同，从而理解为何将某一图形用斜二测画法绘制后，有些边方向和长度都不变、而有些边方向和长度都变了，帮助学生理解斜二测直观图与原图的对应关系。

02 构成空间几何体的基本元素的学习方法

学生在总结各种几何体的特征后，要学会抽象思维，从现实的几何体特征中抽象出点、线、面这些元素，以及这些元素的不同位置关系。特别的，针对线线关系、线面关系，要学会利用生活中的常见物体辅助理解，并用数学语言将这些直观的认识描述出来。

注重观察生活中各种平行线、相交线、异面直线。比如，马路上一排排的路灯、楼梯台阶凸出来的棱和凹进去的交线等；观察各种相交线，特别留意“相交线位于同一平面内”这一现象，为后面观察异面直线打下基础。针对异面直线，学会在生活周围的物品里找实例，比如课桌面的一条边与这条边对面的一条桌腿、操场里的旗杆与教学楼和地面的交线、立交桥等。针对线面关系，可以观察窗框与玻璃的关系、门边与地面的关系等，积累对各种位置关系的直观认识，辅助对概念的理解。

注重将直观认识转化为数学语言。学生在脑海中积累了各种直观认识后，只能说出“感觉是这样的”，但可能难以用数学语言严谨的描述这些“感觉”。用数学语言描述构成空间几何体的基本元素及元素间关系，是学习后续内容所必需的能力。特别的，在斜二测画法中，有许多“看起来不太像”的关系，难以用“感觉”做出正确、严谨的判断，必须用数学符号才能表达清晰。学生应注重复习集合语言，包括属于（∈）、包含（ c）、交（∩）、空集（∅）等符号的含义和用法，特别要区分属于（∈）、包含（c ）这两个符号分别应用于什么对象之间。最后，将所观察到的一个直观现象，同时用文字语言、符号语言、图形语言三种方式描述出来，加深对这一直观现象的理解和记忆，也为后续的进一步学习和理解打下基础。

03 多面体的学习方法

多面体是生活中非常常见的一种几何体，但是生活中的多面体可能形态各异、并非“标准形状”。学生要学会从特殊到一般的抽象思维，从不同的类似多面体的几何体中抽象出“由若干个平面多边形所围成的封闭几何体”这种多面体性质和判定方法，观察和思考多面体的顶点、棱、面有什么数量关系。逐渐理解多面体的相关概念和特征，如正多面体、多面体中的各种对角线、多面体的截面等。

学生可以在家里做一道菜：小葱拌豆腐。在切豆腐的过程中，注重观察刀与豆腐的边（即长方体的棱）的交点可以有多少个，观察在不同交点个数下分别切出哪些形状的截面，加深对体对角线长度与棱长的关系、截面的形状与位置的感性认识。

棱柱是一种相对较简单的多面体，生活中也比较常见，比如粉笔盒、纸盒、高楼等。学生需要从感性认识出发，从数学严谨的角度总结棱柱的特点，学会棱柱中的各种概念，对棱柱进行分类。特别的，要学会严谨的思考四棱柱、平行六面体、直平行六面体、长方体、正四棱柱、正方体这些概念的详细特征，熟练掌握不同的概念所对应的几何体。

学生可以学习使用一些软件来绘制空间几何体，在软件中拖动、改变一些边长、角度等，观察几何体的变化，进一步直观理解不同概念的含义。

棱锥、棱台的学习是基于棱柱的，比如可以将棱锥理解为棱柱上底面缩成一个点、将棱台理解为棱柱的一个底面放大或缩小为相似的形状等。特别的，要学会利用截面的思想，认识正棱锥的斜高、高、侧棱、底边之间的关系。注意区分棱锥与刍甍、棱台与刍童。

04 旋转体的学习方法

旋转体的学习要注意旋转轴、母线等概念，特别的，针对圆锥，要学会区分底面半径、侧面半径（母线），并通过截面的思想，认识到圆锥母线、高、底面半径的数量关系。

在学习旋转体的侧面积时，要学会动手制作旋转体、观察旋转体侧面展开图形的形状，学会分析圆锥轴截面的角度与面积之间的关系、侧面展开图形的圆周角，学会计算扇形面积。

学习球的时候，建议使用地球仪做辅助，观察地球仪上面的经线、纬线长度特点，结合地理知识，在了解纬度含义的同时，学会分析纬线的半径、长度，进而对球的大圆、小圆、截面、半径有更直观的认识。另外，要学会用数学思维思考球的定义，理解“到定点距离相等的点的集合”这种描述方法，严谨的证明出截面形状，训练数学思维。

可以借助飞机航线来理解球面上大圆与小圆的区别。学生可以在网上查阅从北京飞往纽约的航线图，观察航线轨迹，思考为什么飞机不直接沿着纬线飞行，而是往北越过北极飞行。学会取北纬40°夹角的余弦、地球半径、圆周率等近似值，近似估计两种飞行方式的里程数，进而得出结论，再次直观感受球面大圆与小圆的特点。进一步的，学生可以取不同纬线、不同目的地，观察航线轨迹的变化。

05 祖暅原理与几何体的体积的学习方法

祖暅是著名数学家祖冲之的儿子，在研究立体几何中有个重要的结论：“幂势既同，则积不容异。”可以用于求各种几何体的体积。这部分内容综合了前面所学的所有几何体，包括柱体、锥体、台体、球体，需要学生认真复习前面所学几何体的各种特征，比如柱体的分类、截面形状，各几何体的高与底面等。理解好“幂”和“势”的含义，训练空间中的转化思维。

祖暅原理中的难点是如何将形状各异的几何体转化为某一种形状较为标准、体积较为好求的几何体。学生要对柱体截面形状、锥体截面形状有一定的认识和分析，特别是要用到相似比的相关证明和计算，对学生知识掌握程度有一定要求。建议学生回忆相似三角形的各种性质，以及三角形面积的不同计算方法，逐步推导截面之间的关系，训练计算能力和数形结合思维，为后续学习打下基础。