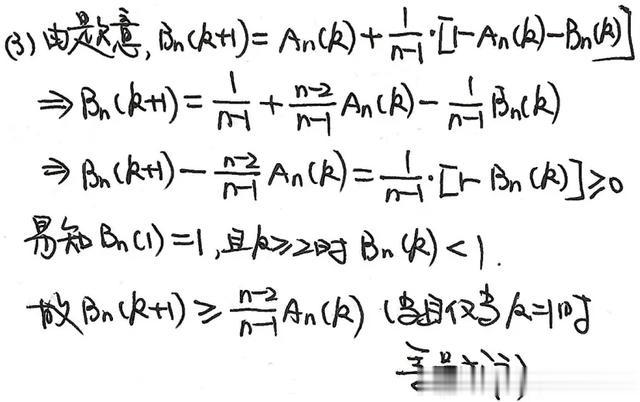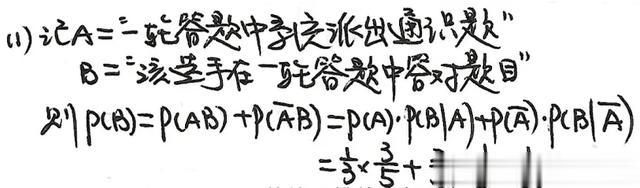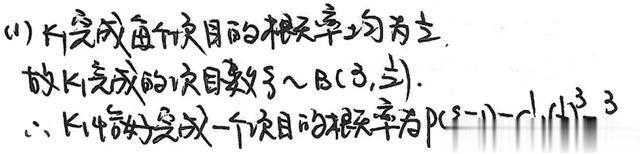1. 基础概率模型

古典概型：结合排列组合的实际问题（如抽奖、分组问题）。

条件概率与全概率公式：疾病检测、信号传输等实际场景的应用题。

事件独立性：多环节事件中独立性的判断与计算（如电路通路概率）。

2. 概率分布与统计

二项分布 vs 超几何分布：区分“有放回”与“无放回”场景（如质检抽样）。

正态分布：结合3σ原则计算概率或参数估计。

分布列与数字特征：求期望、方差，分析决策问题（如游戏得分策略）。

3. 统计推断与数据分析

线性回归分析：计算回归方程、解释系数意义，预测数据（可能结合图表）。

独立性检验（卡方检验）：根据列联表判断变量关联性，注意临界值对比。

分层抽样与系统抽样：设计抽样方案，计算分层抽样的样本比例。

1. 概率与递推数列结合

马尔可夫链简化模型：通过递推关系求稳态概率（如天气预测、状态转移问题）。

2. 实际情境应用题

优化决策问题：结合期望与成本分析最优策略（如保险定价、生产批次选择）。

大数据背景题：如疫情防控中的“混合检测”概率计算，降低检测次数。

3. 条件概率的深度考查

贝叶斯公式应用：已知结果反推原因的概率（如诈骗电话识别、疾病溯源）。

多阶段事件：分步计算复杂事件概率，需画树状图辅助分析。