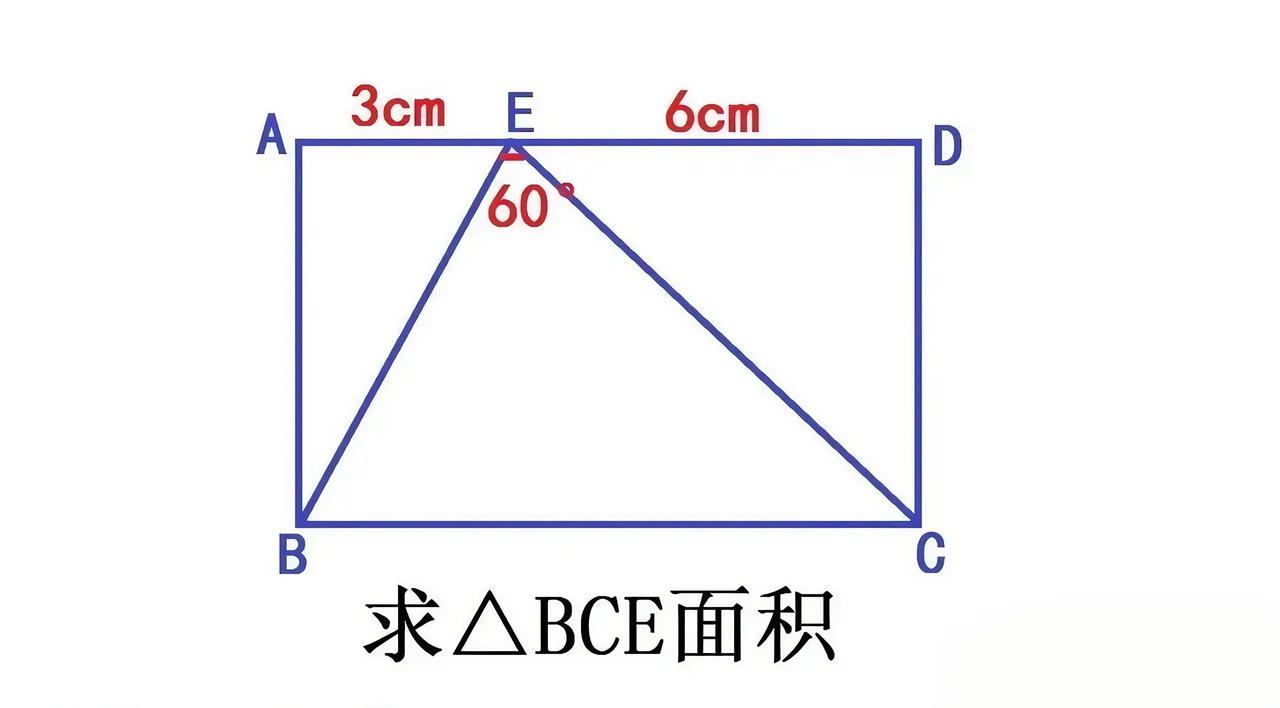
北京一位985高校毕业的老爸,最近在辅导女儿数学时遭遇“滑铁卢”。题目看似简单:长方形ABCD中,E在AD上,AE=3厘米,DE=6厘米,∠BEC=60°,求△BCE的面积。宝爸尝试用常规几何方法分析,却因条件关联隐蔽陷入僵局,最终被女儿一句“你是不是也不会?”怼得哑口无言。 这道题的巧妙之处在于跳出直角思维的惯性。常规解法中,若直接设长方形边长为未知数,会因涉及三角函数或复杂方程而难以推进。但题目中“60°角”的存在暗示了隐藏的等边三角形关系——通过构造辅助线,可发现△BEC的特殊性质。 正确思路需结合几何变换与角度敏感性:将分散的条件(AE=3、DE=6、∠BEC=60°)通过图形旋转或对称重新关联,最终利用等边三角形的面积公式求解。关键在于,通过观察角度与边长的隐性联系,将看似无关的条件转化为可计算的几何模型。 这道题的设计直击代数思维与几何直观的断层,也解释了为何高学历家长易“翻车”——成人习惯用复杂公式,反而忽略了图形中最朴素的角度暗示。正如网友调侃:“这题考的不是数学,是对思维灵活性的终极考验。”
评论列表