60年数学悬案被建筑生破解康威猜想被验证
扔100次,99次「同一面朝上」。
这个由碳纤维和碳化钨(航空材料)打造的“几何怪物”,竟破解了60年数学悬案。
如果这个发明早一点出现,或许“雅典娜”月球着陆器也不会一侧翻就躺平了(doge)。
早在1966年,数学家约翰·康威【图2】和他的搭档查德·盖伊提出了“均匀单稳态四面体”构想。
他们想利用均匀材料制作一个重量分布均匀的四面体,无论将这个四面体如何放置,它总会翻到稳定的那一面朝上。【图3】
几年后,这对搭档通过不断尝试,否定了均匀单稳四面体的猜想:这是不存在的。
但是,如果让重量分配不均匀呢?
后来,康威猜测不均匀配重的单稳四面体应该存在,但他未发表任何证明。
半个世纪以后,这个数学猜想由建筑学者杰尔戈·阿尔马迪【图4】“跨界”证实,还制作出了实物。
所以,这位建筑学者是如何在数学问题上大展身手的呢?
早在60年前,约翰·康威和Guy就提出问题:均匀材质的四面体,能不能无论怎么翻滚,总是“自动落定”在同一个面上。他们的结论是,纯均匀材质四面体做不到这一点。
但是,如果允许质量分布不均呢?虽然圆滑体(像roly‑poly玩具)可以通过在底部加重实现单稳态,可多面体的尖角和平面结构让情况变得复杂很多。
2006年,Domokos团队发现了“gömböc”——这是一个连续曲面、类似硬币的单稳形体,但它不是多面体。康威杂志称,尖锐的四面体是否也可能实现类似特性,引发新一轮思考。
最近,Domokos和研究生Almádi带领团队,用计算机算法“盲搜”成千上万种四面体形状和质量分布,终于找到一种尖顶多面体四面体,只需在某一个面内部加载特定重量,就能实现“无论怎么扔都仅停在这一面”的特性,理论验证康威猜想正确。
更惊人的是这个结构的细节:
- 三条相连棱必须构成钝角,让某面成为唯一稳定面。
- 质心必须落在“加载区”内部,确保翻滚过程中始终回到这个面。
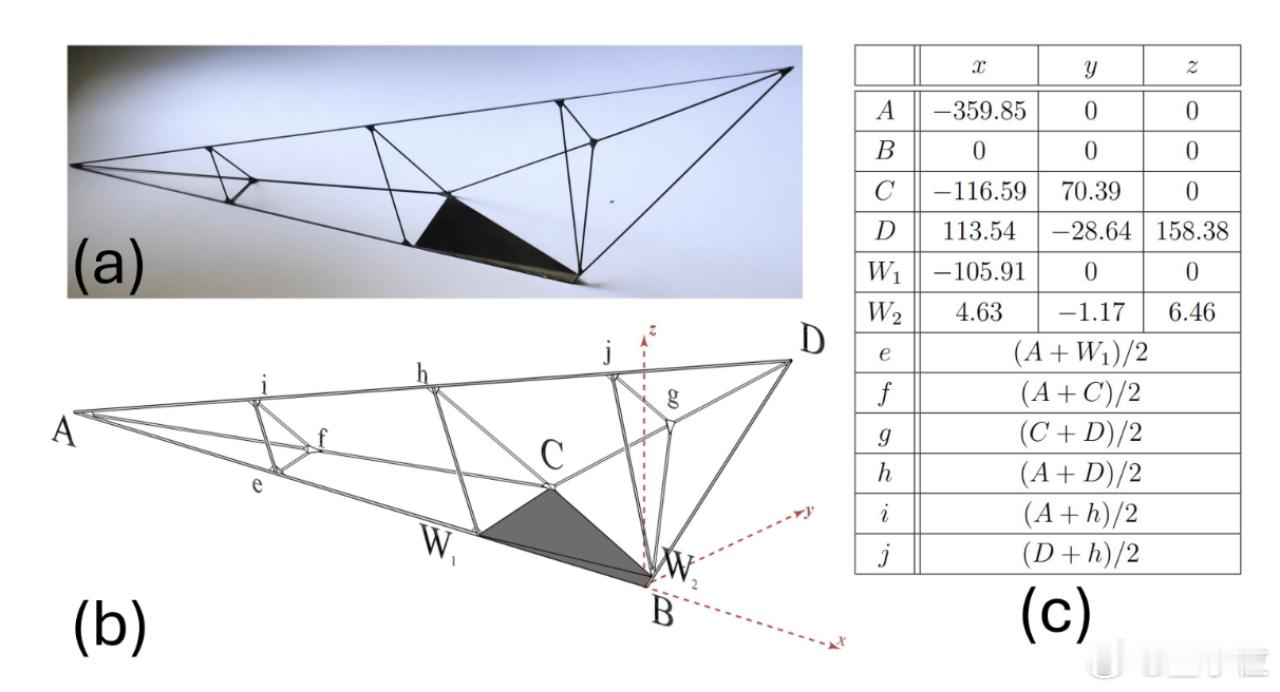
- 实验中他们制作了一个空心碳纤维框架,在某块区域用碳化钨加重,一次误操作掉落的一团胶竟就改变了质心位置,修正后“模型终于能滚回那个面”。【图5】
从手动纸笔到计算机算法,从均匀材质到设计载重区域,从理想模型到真实制造,这项成果不仅实现了一个数学猜想,还为编码平衡机制提供了新思路。
Domokos团队还希望将此成果用于航天器“自动翻正”机制,比如登月器或某些着陆器。【图6】