这是一道初中几何求面积的题目，很多学生没有想到合适的解题方法，思考半天没有办法求面积。 如图所示，AB＝AC，角A等于45度，求三角形Abc的面积？ 我们可以尝试利用三角形面积公式，所以可以过A点作垂线，但是我们把特殊角度分割了，所以还需要继续作辅助线解题。
初中物理易错题里有个有趣的问题：100℃的油和100℃的水，哪个更烫手？从
【142评论】【64点赞】
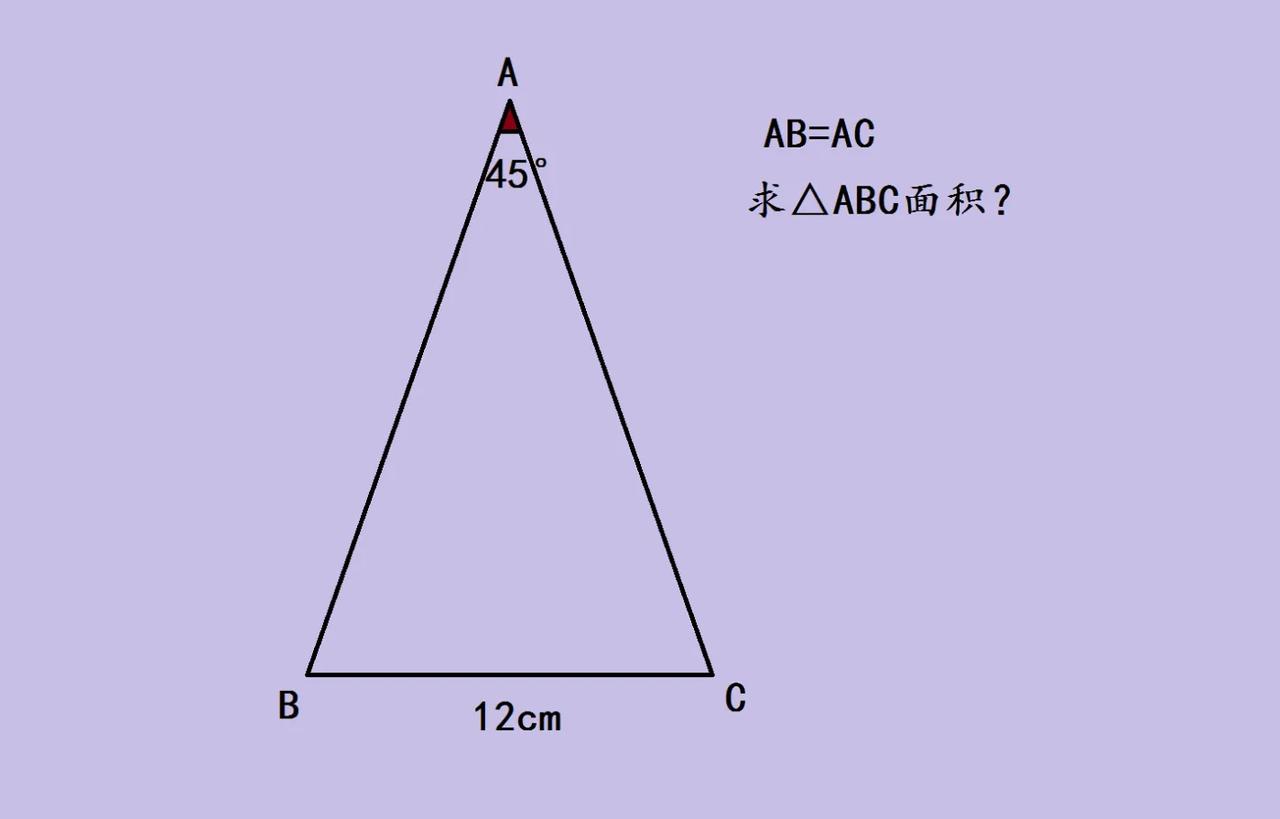
这是一道初中几何求面积的题目，很多学生没有想到合适的解题方法，思考半天没有办法求
大力小学数学吖
2025-06-09 15:10:42
0
阅读：215
赵追
把这个三角形放到圆里面，圆心角都是90度。 这种方法应该更容易理解
用户32xxx27
我觉得可以尝试补个对称型，构造一个等腰直角，然后设腰为未知数，等腰直角中垂线底乘高和现有底乘高构造方程，解出来。可能有更好的方法，但是笨方法也得有思路不是。
用户12xxx32 回复 06-14 01:25
比较简单的解法
用户10xxx73
直接A向BC做垂线，不是更快吗，一个22.5°的正切就出来了高。
赵追 回复 06-15 19:09
确实可以！对九年级学生来说22.5度的正切也不难计算。