一道日本竞赛题,难倒无数人!在三角形ABC中,已知两个非特殊角度,边AB = 1,要求出AC的长度。 很多人看到这道题都懵了,已知角度和一条边,求另一条边,常规思路好像不太好使。其实这道题的破题点在于构造特殊三角形,利用角度关系和正弦定理等知识来求解。 看似简单的条件,背后却隐藏着巧妙的数学逻辑。数学竞赛题就是这样,充满了思维的碰撞和挑战。大家不妨动手算一算,感受一下这道题的魅力,也欢迎在评论区分享你的解题思路!
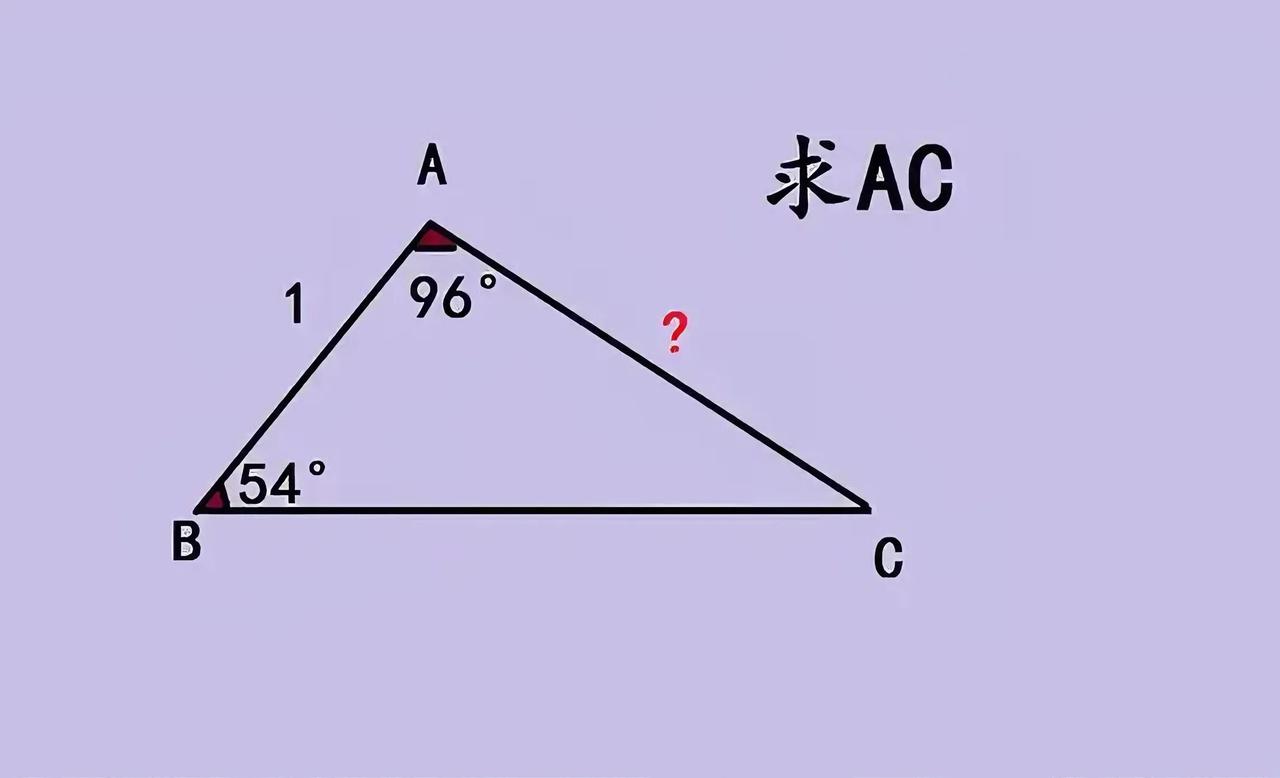
一道日本竞赛题,难倒无数人!在三角形ABC中,已知两个非特殊角度,边AB = 1,要求出AC的长度。 很多人看到这道题都懵了,已知角度和一条边,求另一条边,常规思路好像不太好使。其实这道题的破题点在于构造特殊三角形,利用角度关系和正弦定理等知识来求解。 看似简单的条件,背后却隐藏着巧妙的数学逻辑。数学竞赛题就是这样,充满了思维的碰撞和挑战。大家不妨动手算一算,感受一下这道题的魅力,也欢迎在评论区分享你的解题思路!

评论列表