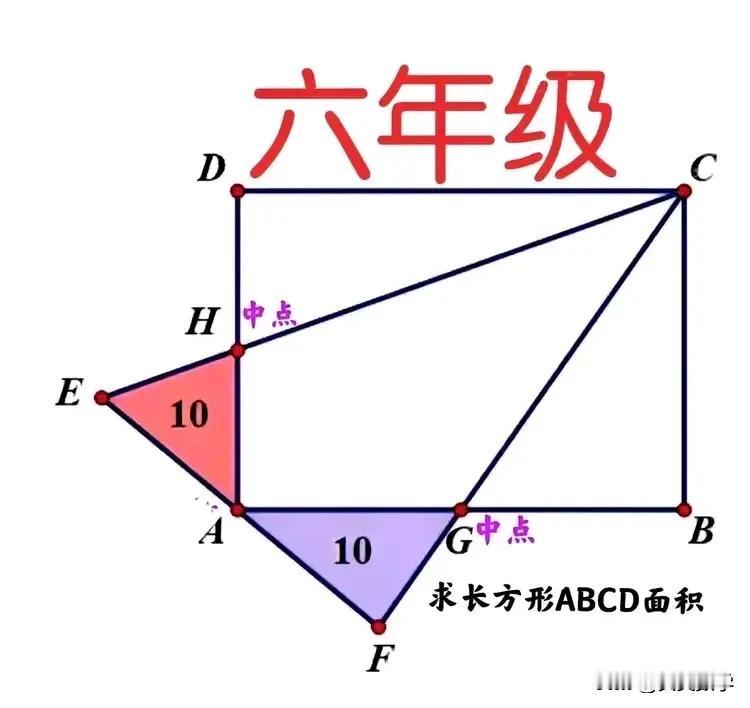
“超级难、极具挑战性！初中生也未必能做出来！”小学六年级数学竞赛题：解题关键在于找出暗含条件“AE=AF”！



如图，H、G分别为长方形ABCD边AD和AB的中点，过点A作一直线、分别与CH和CG的延长线相交于点E和F，三角形AEH和AFG面积均为10，求长方形ABCD的面积。



难点或突破口：说明AE=AF即A为EF的中点。

—————————
提示一：等高（同底）三角形面积比等于底边（高）之比！适合六年级
①连接AC，则S△ACH=S△ACG，从而由S△AEH=S△AFG可知，S△ACE=S△ACF，故AE=AF即A为EF的中点。
②连接HG，由S△AEH=S△AFG和AE=AF可知EF⫽HG。
③连接BD、与CH相交于点M，则BD⫽HG⫽EF。
④连接DE和AM，则S△DEH=S△AEH=10。
⑤由EF⫽BD可得，S△ADE=S△AME，从而S△AMH=S△DEH=10，这意味着H为EM中点，从而S△DMH=S△DEH=10。
⑥连接BH，S△BCD=2S△BDH，故△BCD底边BD上的高为△BDH底边BD上高的2倍。从而S△CDM=2S△DMH=20，也即S△CDH=30。
⑦因此S长方形ABCD=4S△CDM=120。



提示二：平行线段比或相似比！适合初中生


友友们，怎么看？欢迎留言分享！