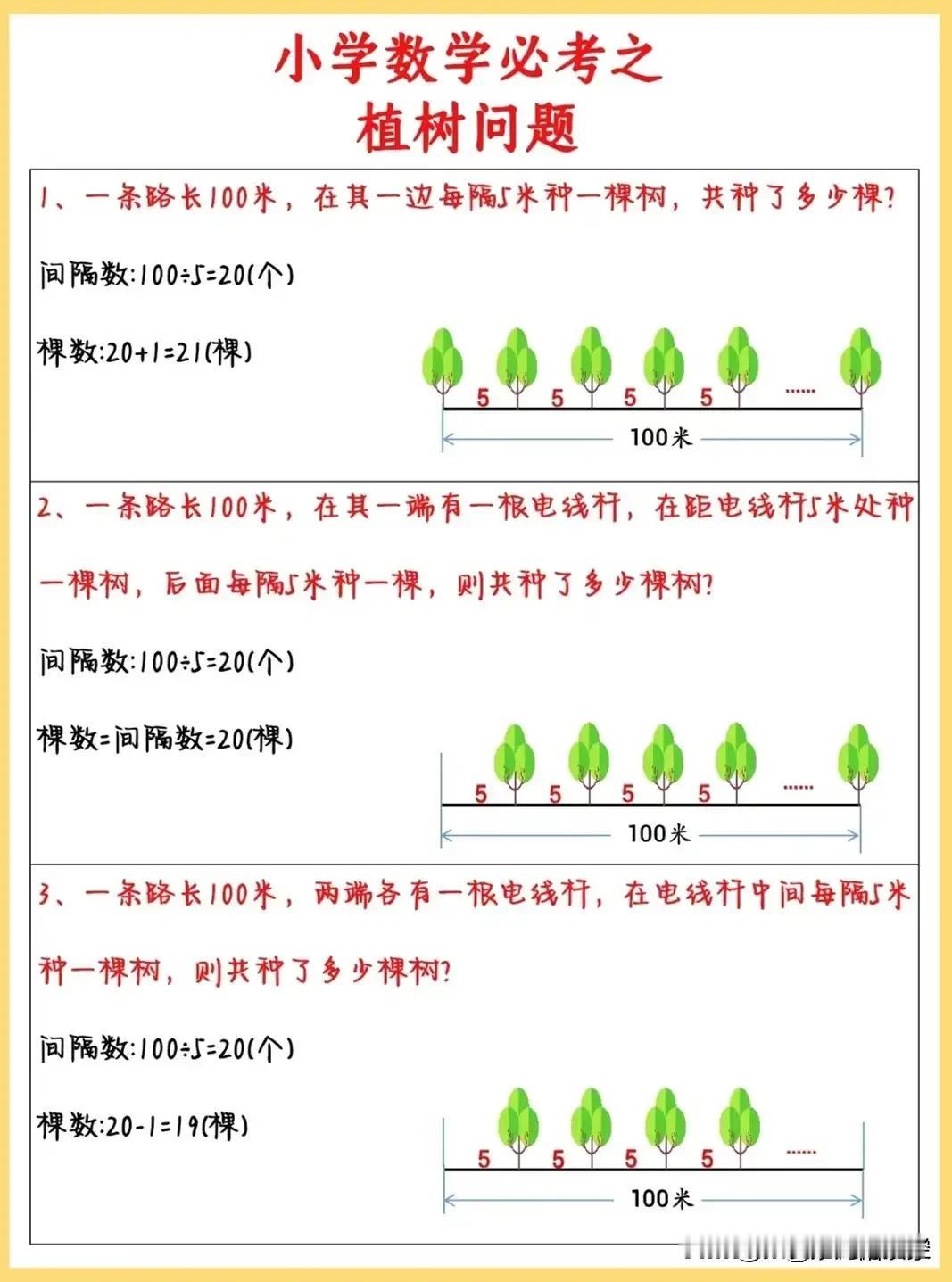
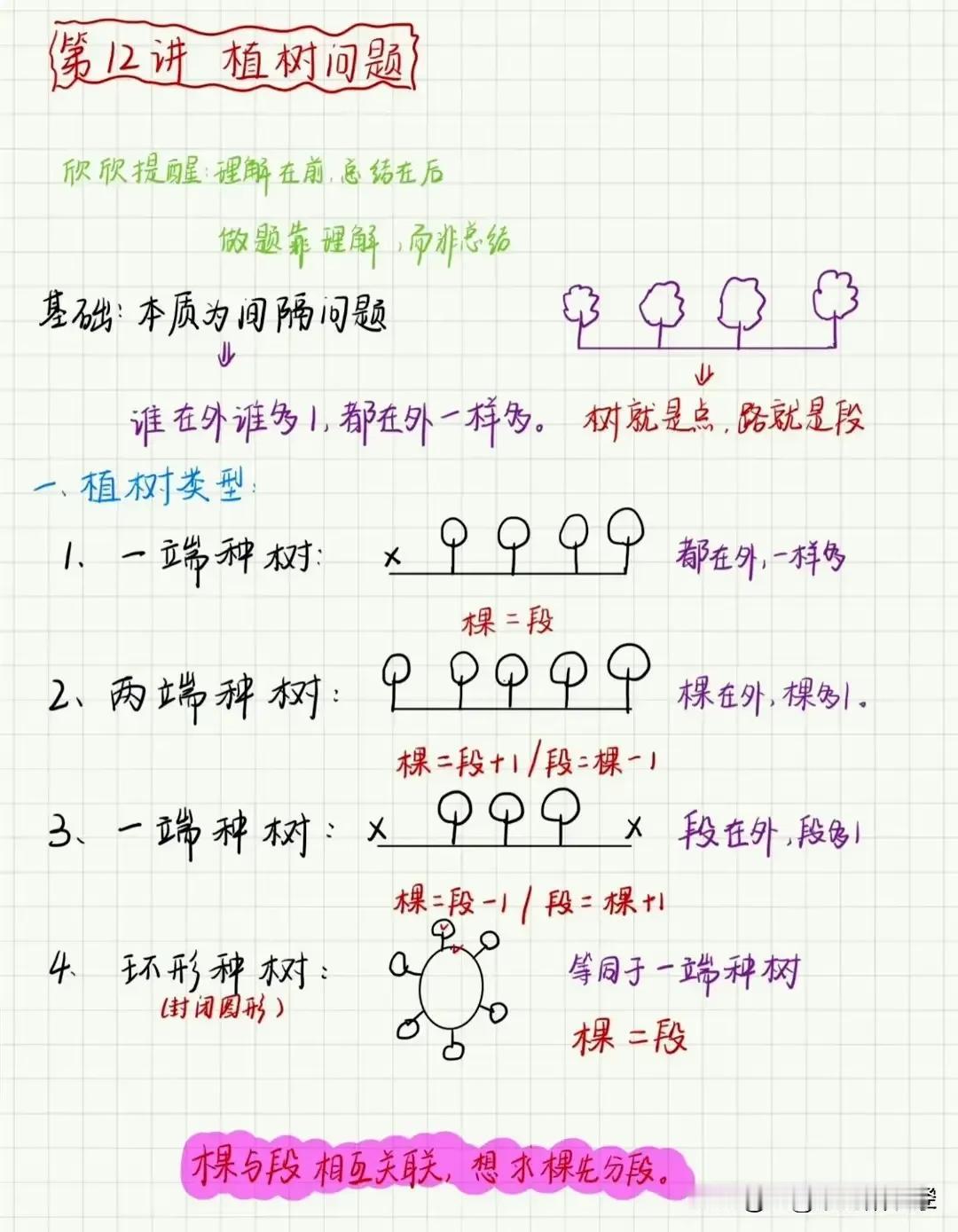
厉害了,终于有数学老师把小学常考的应用题汇总出来了,比如“植树问题”再难,无非就是搞清楚“间隔和棵树”的关系,家里有孩子的,家长再忙也要给孩子收藏起来慢慢学! “植树问题”之所以成为小学数学中的一个难点,很大程度上是因为它涉及到了“间隔和棵树”这一核心关系的理解与应用。许多孩子初遇此类题目时,往往会被题目中纷繁复杂的情境所迷惑! 比如单侧植树、两侧植树、闭环植树,甚至是上楼问题(这里上楼问题虽非字面意义上的植树,但其数学本质与植树问题相通,即通过计算间隔来确定总数),这些看似不同的问题,实则都归属于“植树问题”的范畴,其核心都在于准确理解和运用“间隔与棵树”的关系。 以一个新颖的例子来说明:假设小明家住在五楼,每层楼梯有16级,小明从一楼走到五楼,他总共需要走多少级楼梯?这个问题初看之下与植树问题无关,但仔细分析,我们可以发现其中的奥秘。 将每一层楼梯看作是一段“间隔”,而小明从一层走到另一层的过程,就像是“种下一棵树”。由于是从一楼走到五楼,相当于是在四个“间隔”(一层到二层、二层到三层、三层到四层、四层到五层)中“种树”。 但需要注意的是,这里的“种树”是从第一层开始计算的,即第一层到第二层是第一段“间隔”,也是第一次“种树”的开始,因此总数应为4段间隔对应的楼梯数相加,即4*16=64级。这样一来,原本抽象复杂的“上楼问题”就转化为了直观的“植树问题”,孩子们只需掌握“间隔与棵树”的关系,便能轻松应对。 再来看一个关于单侧植树的例子:一条长100米的道路,每隔5米种一棵树,两端都种,问一共需要种多少棵树?这里,“间隔”是5米,“道路总长”是100米,通过计算可知有20个间隔,但由于两端都要种树,所以树的数量应为间隔数加1,即20+1=21棵。这个例子再次证明了“间隔与棵树”关系的重要性。 无论是上楼问题还是单侧、两侧、闭环的植树问题,只要孩子们能够把握住“间隔与棵树”这一核心关系,就能做到举一反三,轻松应对小学数学中的各类应用题。家里有孩子的,家长再忙也要收藏起来给孩子学习一下,更多小学应用题可以下方链接走起! 小学数学应用题训练