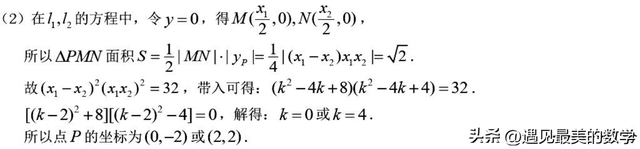解析几何复习需 “基础为根，方法为干，运算为叶”，在理解核心概念的基础上，通过典型例题总结通法，强化运算能力和数学思想的应用，同时注重实战训练与错题反思。考试中需保持耐心，先完成基础和中档题，压轴题可分步得分（如写出联立方程、韦达定理等步骤分），避免因畏难情绪放弃。

关注高频考点与题型，总结解题模板

高考解析几何题型相对固定，需针对性训练：

高频考点分类

基础题：求曲线方程、离心率、渐近线、抛物线焦点与准线等。

中档题：直线与圆的位置关系（如切线方程、弦长计算）、直线与圆锥曲线的位置关系（如中点弦、弦长、面积）。

压轴题：圆锥曲线中的定点、定值、最值、存在性问题，与向量、导数、不等式等知识的综合题。

典型题型模板

定点问题：设动直线方程为y=kx+m，通过条件找到k与m的关系（如m=k+1），代入后消去参数得定点坐标。

定值问题：先通过特殊位置（如斜率为 0 或无穷大）猜测定值，再一般化证明（利用韦达定理代入化简）。

最值问题：几何法（利用圆锥曲线定义转化为距离最值）或代数法（建立目标函数，用导数、均值不等式等求最值）。

存在性问题：假设存在，设参数后联立方程，结合判别式和已知条件求解，若有解则存在，否则不存在。

数学思想方法：提升解题思维

解析几何复习需渗透以下思想，避免机械刷题：

数形结合思想

画图分析几何条件（如焦点位置、直线与曲线交点分布），辅助理解代数运算的几何意义（如判别式对应交点个数）。

函数与方程思想

将几何问题转化为方程或函数问题（如求弦长最值转化为二次函数最值），利用函数性质求解。

分类讨论思想

涉及直线斜率是否存在、曲线焦点位置（如椭圆长轴在x轴或y轴）、参数范围（如双曲线中a与b的大小关系）时需分类讨论。

转化与化归思想

复杂问题简单化（如将一般圆锥曲线问题转化为标准形式）、陌生问题熟悉化（如利用向量条件转化为坐标运算）。

实战训练与错题总结限时训练，规范答题

解析几何大题通常位于试卷后两题，需在限时内完成（如 20 分钟内），训练时注意书写步骤的逻辑性（如先设方程、再联立、写判别式和韦达定理、最后代入求解），避免因跳步失分。

整理错题，分析错因

常见错误类型：概念不清：如混淆椭圆与双曲线的离心率范围、抛物线开口方向判断错误。运算失误：联立方程消元错误、韦达定理代入时符号错误、分式化简出错。忽略条件：未考虑直线斜率不存在的情况、未验证判别式导致增根。针对错因专项突破：如运算薄弱可每天练习 5 道联立方程求韦达定理的题目，概念不清则制作 “易错点清单” 强化记忆。

研究高考真题，把握命题趋势

分析近 5 年真题中解析几何的题型变化（如是否更侧重抛物线与直线的综合、是否出现与平面向量结合的问题），总结命题规律，针对性训练。