中，每当两个原子轨道发生重叠时，总会形成一对轨道：一个能量较低，另一个则是能量较高。

、化学反应性以及电子结构这一规律不仅是理论上的抽象推演，还在实际材料和分子中得到广泛体现。例如，氢分子中两个这种对应关系决定了，也解释了为什么某些分子在特定电子数下稳定，而在额外电子填充到反键轨道时则变得不稳定。

轨道重叠原理、量子力学对称性机制、实际案例分析LCAO）相加时，波函数在核间区域发生相长干涉，电子密度增大，核间吸引作用增强，从而形成能量低于原子轨道的成键轨道。相减时，波函数在核间区域发生相消干涉，电子密度减小，甚至出现节点，导致原子间的排斥作用增强，从而形成能量高于原子轨道的反键轨道。

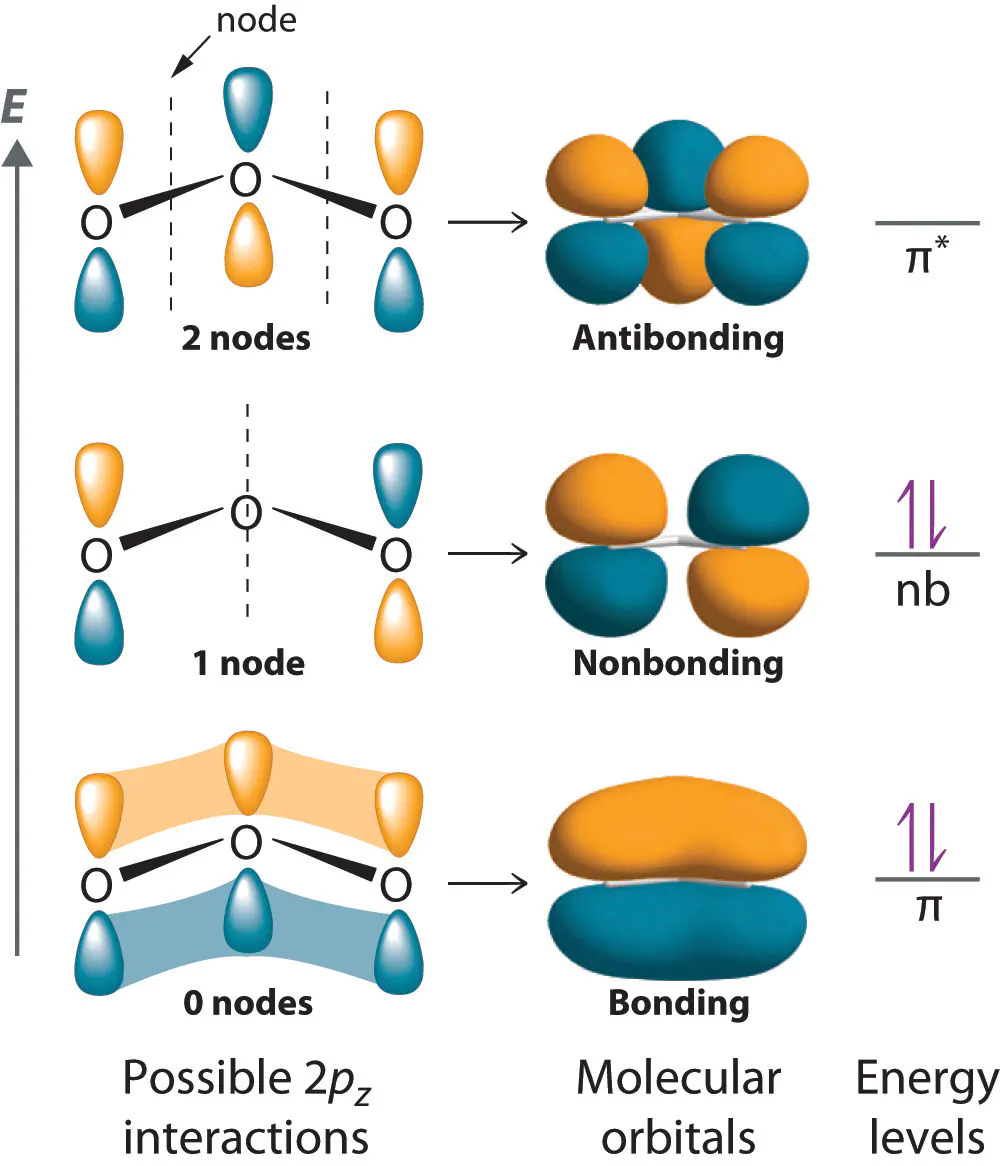
这种成键–反键的配对关系，本质上来源于波函数的干涉规律这意味着每当两个原子轨道发生重叠时，体系必然会同时产生稳定化与去稳定化两种趋势，分别对应于成键轨道与反键轨道的形成。

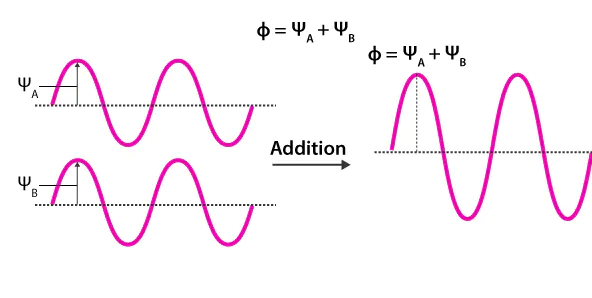
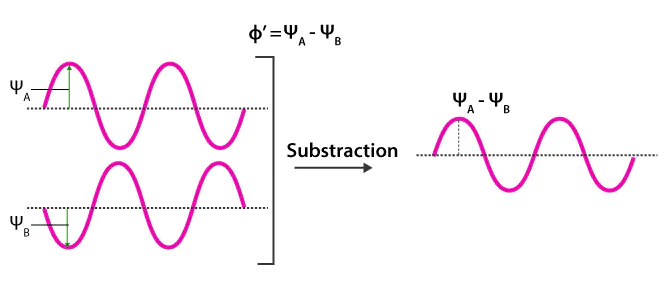
量子力学正交性与轨道数守恒

LCAO方法中，如果我们用两个原子轨道构建分子轨道，那么最终必须得到与基函数数目相等的分子轨道。

。在希尔伯特空间中，波函数构成一个完备的基底集，任意两个波函数的线性组合都可以生成一组新的正交基底。这种正交性要求保证了轨道不会重复计数，也不会凭空消失。

。这也是分子轨道理论中“轨道数守恒”原则的数学体现，即分子轨道数目等于组成它的原子轨道数目。

对称性与能量分裂机制

。两个原子轨道的叠加，往往会生成对称性不同的两个新轨道：一个在原子核连线上具有对称性，另一个在连线上具有反对称性。

这种对称性的差异，决定了电子密度的分布与能量差异1s轨道叠加后，σ1s轨道具有对称性，电子密度集中在核间区域；而σ1s*轨道则具有反对称性，核间形成节点，能量显著升高。

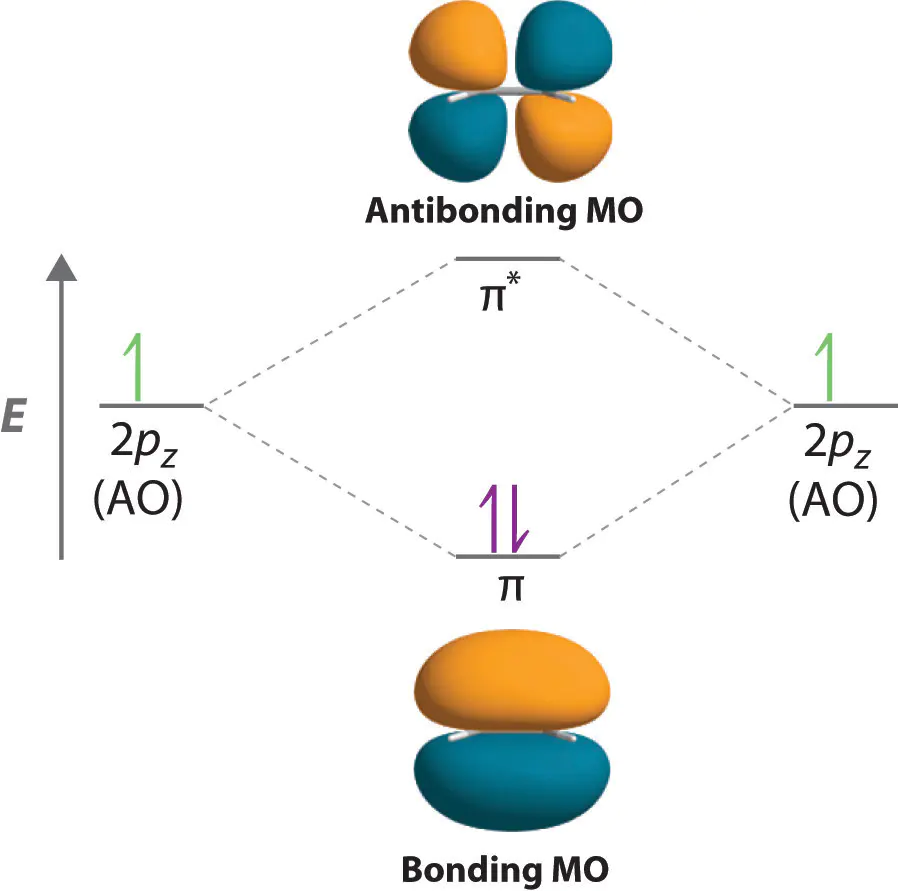
这种对称性差异也导致了轨道能量的分裂然而，若电子数继续增加而占据反键轨道，则体系能量上升，分子稳定性减弱。这种分裂机制不仅解释了分子的成键特性，还为理解反应活性与分子稳定性提供了重要依据。

典型案例分析

H1s轨道叠加形成σ1s与σ1s轨道。当两个电子填充在σ1s轨道时，体系能量降低，氢分子稳定形成。

在更复杂的体系中，这种对应关系依然成立。例如，在₂分子中，₂的顺磁性。在过渡金属配合物中，金属由此可见，。

在化学与材料研究中的应用意义

例如，亲核反应往往发生在分子在材料科学中，能带结构的形成同样源于轨道叠加。大量原子轨道在周期性晶格中叠加，形成连续的能带，其中价带可视为成键态的延伸，而导带则包含大量反键态。

不仅是分子层面的规律，也是固体电子结构理论的重要基础DOI:10.1088/1361-6528/abcf6d

未来发展与跨科学研究

方法与第一性原理计算能够更精确地描述轨道能量与空间分布，使得成键与反键轨道的对应关系不仅停留在定性解释层面，还可以通过数值模拟精确呈现。

在跨学科领域，成键与反键轨道的概念正广泛应用于分子电子学、光电催化与量子材料研究。例如，在光催化分解水中，光生电子从成键轨道跃迁至反键轨道，进而驱动化学反应；在分子电子器件中，反键轨道的可调性决定了分子导电性能。因此，成键与反键轨道的对应关系不仅是基础科学问题，更是推动新兴技术发展的理论基石。

总结

，这一规律来源于波函数叠加的数学必然性、量子力学的正交性守恒以及对称性导致的能量分裂机制。

随着理论与实验方法的发展，这一轨道对应关系将在更广泛的领域中被深入应用，并继续作为理解物质本质的重要理论支柱。