佛教有一句非常有启发性的话语:"用肉眼看世界,只见名利;用天眼看世界,只见轮回;用法眼看世界,见因果;用慧眼看世界,见幻象;用佛眼看世界,充满慈悲。"
有数学老师说过这样一句话:中点坐标公式是被严重低估的王炸公式。关于这个公式的推导,请看下图:
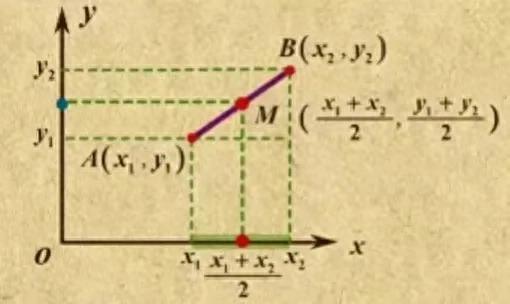
本来我觉得无话可说,可是看见了下图,发现还是有同学不理解这个公式,所以就再啰嗦几句,解释一下。

大家看见了什么?我看见了降维打击!
既有大小又有方向的量,物理学家称为矢量,数学家称为向量。只有大小没有方向的量,称为标量。
上图的线段AB可以看成向量,是二维的。求线段中点M的坐标比较棘手。在问题没有解决之前,可以退一步海阔天空。我们暂且降低难度,考虑一维问题。数轴是一维的,我们考虑数轴上的线段AB如何求中点坐标。
比如点A坐标是6,点B坐标是14,求线段AB的中点M的坐标。(因为数轴是一维的,所以一个数就能够确定点A在数轴上的位置)
这个问题简单,答案当然是(6+14)÷2=10啦。于是我们有了一个领悟,求两个数的算术平均数的几何意义就是求数轴上线段的中点坐标。
有的同学有点担心,如果两个数一正一负,那么平均数和中点还能一一对应吗?
算一下就知道了。比如-1和3,算术平均数是1,中点是不是1呢?不管你是用绝对值的几何意义去想,还是画个数轴来考察,你会发现中点是1。这个方法对数轴上的全体实数都是成立的。
一维问题想明白了,可以进一步考虑二维问题了。回到中点坐标公式推导图,我们看见了降维打击。

求中点M的坐标可以分为两步走,先求横坐标,再求纵坐标。把点A,B投影到x轴,分别得到点x₁和点x₂,二维点A(x₁,y₁)遭到降维打击,被转化为数轴上的一位维点x₁了。我们已经把一维问题想明白了,所以通过转化,轻松求出了中点M的横坐标是(x₁+x₂)÷2。
同理可证,中点M的纵坐标是(y₁+y₂)÷2。
所以我们就得到了中点坐标公式:
已知点A坐标(x,y)和点B坐标(x,y),则线段AB的中点M的坐标为

透过中点坐标公式推导图,还能看见中位线。构造一个以AB为斜边的直角三角形,过斜边中点M可以作出两条中位线。我们知道三角形的中位线平行于底边且等于底边的一半。这样想也能想明白中点坐标公式。
如果你把线段AB看成单位圆的半径,那么半径在x轴的投影就是cos x,在y轴的投影就是sin x。如果动点p在单位圆的圆周上作匀速圆周运动,那么点p在x轴的投影就是余弦函数的图像,在y轴的投影就是正弦函数的图像。这样考虑问题,就把数学和物理结合起来了,抽象的数学有了具体的物理含义和应用。

单位圆
佛教有五眼的说法,爱因斯坦说你能观察到什么取决于你持有的理论。如果理论水平有五种境界,就可以对应五眼,分别看到不一样的风景。
此时此刻,想到了诗圣杜甫的《望岳》,“会当凌绝顶,一览众山小”。
同学们,我们要掌握更多的知识和理论,居高临下,势如破竹,可以看得更清楚,看见更美的风景。
射影定理说到直角三角形,不禁想到了著名的射影定理。这个定理的发现,要归功于伟大的《几何原本》作者欧几里得。
请看下图:
在△ABC中,∠BAC是直角,
AD⊥BC垂足是D,则

射影定理基本图
(1)AB²=BD·BC
AC²=CD·BC
(2)∵BD·BC+CD·BC=BC²(射影定理)
∴AB²+AC²=BC² (勾股定理)
(3)AD²=BD·DC
(4)BD:DC=AB²:AC²
说明:BD和DC分别称为AB和AC在斜边BC上的射影,故结论(1)称为射影定理,它可以用文字表述为:在直角三角形中,每一条直角边都是它在斜边上的射影和斜边的比例中项。
同样,结论(3)也可用文字叙述为:在直角三角形中,斜边上的高是两直角边在斜边上的射影的比例中项。
结论(4)也可用文字叙述为:在直角三角形中,两直角边的平方比等于它们在斜边上的射影之比。
为什么有这些结论呢?这些结论都可以用相似三角形的性质推导出来。
我们知道,如果两个三角形相似,那么对应角相等,对应边成比例;面积之比等于相似比的平方。
三角形有三条中位线,首尾相连构成一个小三角形。4个小三角形是全等三角形,它们和原三角形是相似三角形。即小三角形和原三角形的相似比是1:2,面积比是1:4,即1²:2²。我们用一个简单的例子验证了相似三角形的面积比等于相似比的平方。
构造相似三角形的常用方法是平行和垂直。所以图中简单的向底边作垂线,就构造出三个两两相似的直角三角形。
根据对应边成比例,很容易推出上面的结论。
11岁的爱因斯坦巧证勾股定理勾股定理的证明方法早已超过400种,欧几里得的证明使用了下图。

图源《数学天方夜谭》
欧几里得的证明很复杂,要把上图旋转一下,直角三角形的斜边为底边,看起来像跳舞的正方形,添加很多条令人眼花缭乱的辅助线,看起来像风车,这里就不介绍了。
李永乐老师在视频里介绍了爱因斯坦11岁时证明勾股定理的方法。
直角三角形△ABC的直角顶点是A,作垂线AD⊥BC,就构造出三个相似直角三角形,它们的斜边分别是a,b,c。显然,△①+△②=△③
如上图所示,这些三角形和正方形都是相似的,它们的相似比可以设为常数m,得
正方形面积为a²,b²,c²,与之对应的三角形面积为ma²,mb²,mc²,∵△①+△②=△③
∴ma²+mb²=mc²,
两边约去常数m,得
a²+b²=c²,命题得证。

爱因斯坦的证明是非常巧妙的。勾股定理是直角三角形的一个天然属性,不论是用射影定理来证明还是爱因斯坦的证明,都使用了相似三角形的性质。由此看来,勾股定理是相似三角形的众多推论之一,是源于相似三角形性质的几何瑰宝。
科学尚未普及,媒体还需努力。感谢阅读,再见。
