 回忆杀之八十年代
回忆杀之八十年代现在流行的穿越题材作品,不但有穿越到古代的爽文爽剧,还有重生或穿越到八十年代的。看来八十年代还是一个很有吸引力美好的年代。
八十年代可以说道的太多了,这里只说一下1984洛杉矶奥运会。
在电视还很稀罕的年代,我是在邻居家的电视上观看了洛杉矶奥运会开幕式。这是新中国第一次参加奥运会,开幕式的精彩表演给我留下了深刻的印象,特别是团体操表演居然用队形摆出来美国本土的国界线。
关于奥运会的报道,我的信息来自《世界之窗》,看起来像一本书,其实是期刊。有一则报道说,你购物排队的时候,千万别排在某人后面,因为他是奥运会的采购。还有报道的标题是:许海峰一声枪响,看台上升起五星红旗。
因为1979年苏联入侵阿富汗,所以我国和美国等多国都抵制了1980莫斯科奥运会。作为报复,苏联和东欧国家及东德(民主德国)抵制了洛杉矶奥运会。也因此我国取得了15枚金牌的好成绩。
不过这些都是浮云,今天的主题是致敬美国科普大师马丁·加德纳的经典著作《啊哈!灵机一动》(Aha!Insight,上海科学技术文献出版社)。
我和这本书的亲密接触来自于邻居的热情推荐,这本书像一泓清泉滋润了我的心田。本书精彩内容很多,弱水三千,吾独取一瓢饮,谈谈第一次知道相交弦定理的故事。
请看书中的题目呈现:(隐蔽的尺寸)
在市广场中央有一片很大的圆形憩息地,市议会拟在该地建造一个菱形浅水池。
多丽丝·赖特市长看到这一计划,她找来了建筑师:
赖特市长:我喜欢呈菱形的水池,用红瓷砖砌成,不知这水池每边有多长?
建筑师弗兰克·劳埃德·朗被问住了。
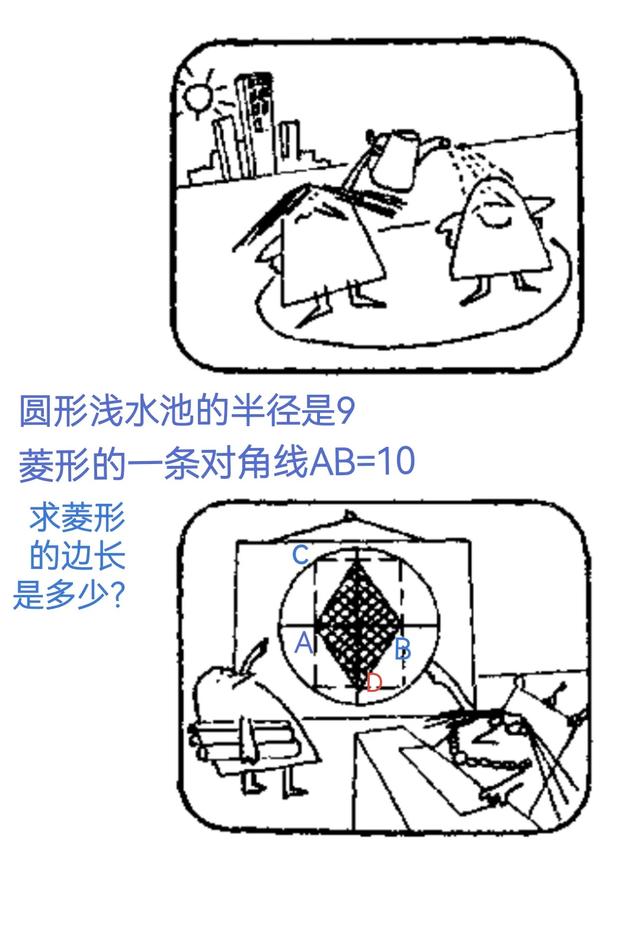
朗先生:让我们考虑一下。从 A 至 B 是5米,从 B 至C是4米。唔,应求出 BD,也许我需应用毕达哥拉斯定理。
朗先生正疑惑不解,市长阁下忽叫起来。
啊哈!
赖特市长:啊哈!水池每边恰是9米,这是毫无疑问的。
朗先生:我的天,怪不得你姓赖特,我姓朗"。
"赖特( Wright )一姓与正确的( right )一词同音;朗( Wrong )一姓与错误的( wrong )一词同音
——译注
有了什么简单的好主意使这个问题迎刃而解?
既是对角线又是半径
赖特夫人忽然悟到水池每边即为矩形的对角线。这个矩形的另一条对角线就是圆形憩息地的半径。而矩形的两条对角线是相等的,所以水池每边边长就是圆半径的长度。半径是5+4=9米,因此水池每边也是9米,无需应用毕达哥拉斯定理。
你再找一种更简便的方法试试看,这样你就更能体会我们这种解法的优点。如果你仅应用毕达哥拉斯定理和相似三角形,其解法一定很冗长、繁琐。但你如果想到下列平面几何定理:一圆内两弦相交,一弦的两部分之积等于另一弦两部分之积,那么就可以得出稍为简短的解法。根据这一定理,可以求得直角三角形的高为√56,再应用毕达哥拉斯定理,算出直角三角形的斜边为9。
有一个与此密切相关的问题,那就是诗人亨利·朗费罗在其小说《卡瓦诺》中所提出的有名的水仙花难题。当水仙花花茎垂直时,花朵伸出湖面10厘米。如果把水仙花拉向一边,使花茎保持直线,花朵沾水的位置离原先花茎接触湖面的位置为21厘米,问水深多少?

水仙花难题
要解这个问题,可以先画一张如图4(见52页)那样的图形。此图与水池问题的图相似。我们要确定的就是 x 的长度。与水池问题一样,这个问题也不止有一种解法。若你还记得两弦相交的定理,问题的解决将是轻而易举。
读后感八十年代读此书时,我还是懵懂少年。第一次知道了相交弦定理,感觉很神奇,留下了深刻印象。
水池问题其实是考察答题者的数学想象力。当你发现菱形边长=对角线=半径的时候,有一种恍然大悟的愉悦心情。如同开天眼一样的洞察力,可以超越繁琐的几何计算而直达彼岸。
如果你没有发现这种漂亮的解法,那么可以用相交弦定理计算边长。
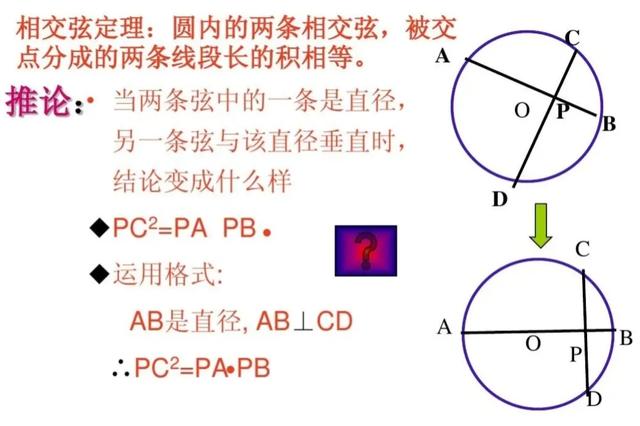
圆内两弦垂直相交于点A,直径AB被分为4和14两部分。由相交弦定理的推论可知:
AC²=4×14=56,所以AC=√56(据题意取算术平方根)
再由勾股定理可得
AC²+5²=边长²
所以,边长=√(56+25)=9
水仙花问题用相交弦定理解决很容易,关键在于看到题目的隐圆。

由相交弦定理的推论列方程:
21²=10(2x+10)
这是一个一次方程,容易解得441=20x+100
20x=341
x=341/20=17.05
由本题可知,已知弓形的底和高,可求得半径。
学校里教的相交弦定理是这样的画风。请看下图。

上面是相关例题。

后来通过进一步学习,知道了圆幂定理。
用几何应用题致敬经典题目呈现:小明同学平时无事好作非非想,总觉得吃别人嚼过的馍不香。学习了二次方程后,小明上体育课时看着操场的百米跑道发呆,突然想到一个问题。他想,如果地球是标准的球形,那么百米跑道应该是一段圆弧而不是直线。圆弧和直线构成了一个弓形,那么这个弓形的高度该是多少呢?
晚上放学回家,小明同学就开始着手解决这个问题了。
地球半径已知是6371公里,单位要统一,百米跑道的一半是0.05公里,设弓形的高是x,根据相交弦定理的推论容易列方程:
x(12742-x)=0.05²......①
解方程难度在于数字太大,所以小明就借助科学计算器解题。
小明同学借助科学计算器得到了答案,并给我们出了一道选择题:
所求弓形高度约等于( )。
A. 1.96km B. 1.96m
C. 1.96mm D. 1.96μm
请选择你的答案。
用配方法致敬杨辉杨辉是南宋数学家,位列宋元四大家之一。其余三位数学家是秦九韶、李益和朱世杰。
中学课本的杨辉三角形在国外称为帕斯卡三角形,在数学史和专业教科书里被称为贾宪三角形。北宋数学家贾宪应该感谢杨辉,如果没有后者的引用,那么我们对贾宪一无所知。
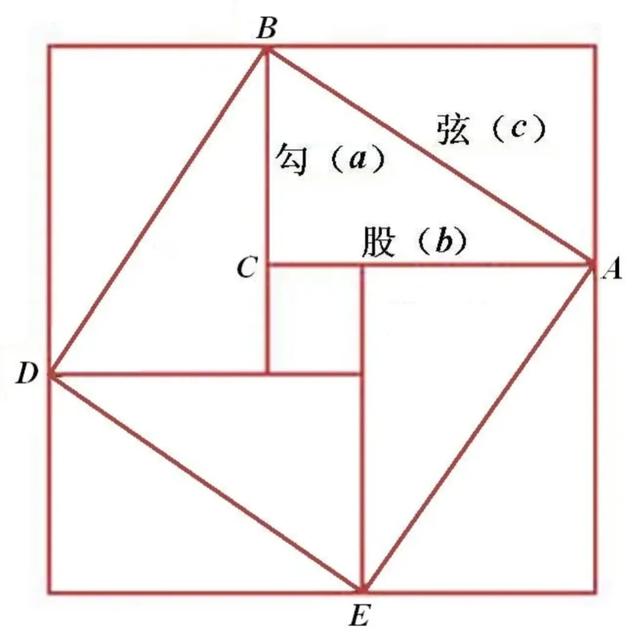
杨辉解二次方程的方法叫做四因积步法,图形来源于赵爽弦图。古代数学家善于用几何法解决代数问题。杨辉的配方法的代数意义就是下面的恒等式:
(a+b)²=(a-b)²+4ab......(1)
既然今天的主题是怀旧和致敬经典,那么我们就选择用杨辉方法解二次方程。
首先设元:根据方程x(12742-x)=0.05²......①,设a=12742-x,b=x,则有a+b=12742,a-b=-2x+12742=-2(x-6271),ab=0.05²=0.0025
把数据代入恒等式(1)得
12742²=[-2(x-6371)]²+4×0.05²
12742²=4(x-6371)²+0.01
4(x-6371)²=12742²-0.01
(x-6371)²=¼(12742²-0.01)
x-6371=½·[±√(12742²-0.01)]
∵12742²=162358564
∴被开方数=162358563.99
∴平方根=±12741.999999607
596923553838480050054462335
再除以2,得
±6370.9999998037984617769192400250272311677
解这个一次方程,得
符合题意的根是
x=0.0000001962015382230807599749727688323(km)
换算成毫米,得
x≈0.196(mm)
你的选择选对了吗?
题目完成后的工作:复盘
如上图所示,OCBD是一个扇形,如果把它看作小明问题的扇形,那么它的圆心角是多少度呢?
地球半径太大了。318国道起点上海市黄浦区,终点西藏自治区日喀则市,途经成都,全长5476公里。
漠河到曾母暗沙是我国南北的最远的距离,约5500公里,还是够不着地球半径。
北京到南京自驾路线查询:总里程为1042公里,开汽车大约耗时为11小时28分钟。大约要跑3个往返里程,才接近地球半径。
要求扇形圆心角,先求它的半角。用正弦函数的概念来看,相当于你开车跑一条笔直的高速公路开了6371公里,海拔高度才增加50米。这个坡度非常接近零度角。
我们可以用反正弦函数来求这个半角。
arcsin(0.05/6371)
=sin⁻¹(0.05/6371)
=7.84806...×10⁻⁶
=0.00000784806(rad)
=0.0004496607(deg)
弧度与角度换算:
0.00000784806×180÷π
=0.0004496607°
所求圆心角为
0.0004496607°×2
=0.0008993214°
小明问题相当于是用内接正n边形逼近圆。怎么算n的值呢?
用r=6371可得地球周长是40030.17km,除以0.1km得
40030.17÷0.1=400301.7
或者可以这样求n的值:
360÷0.0008993214
=400301.82
也就是说,用一个内接正40万边形代替圆,产生的误差非常小,可以忽略。
知识概括:圆幂定理相交弦定理是一个漂亮的定理,让人意外又散发魅力。在给人欣喜的同时,一个疑问油然而生,它为什么成立?如何证明呢?
请看下图,为初学者解惑:

原来可以把两条相交弦连接为圆内接四边形,圆内弦可以看作对角线,构造出两对相似三角形。由相似三角形的性质轻松推导出相交弦定理。证明三角形相似的关键是圆周角定理,即圆内弦所对同侧的圆周角彼此相等,两侧的圆周角互补。
还可以这样证明,请看下图:

图源B站
把相似三角形放大后构造全等三角形,再拼接成平行四边形。
圆幂定理请看下图:
 一个联想
一个联想此时此刻,想到了天文学家开普勒分圆推导出圆面积公式的往事。
有图有真相,请看下图:

开普勒把圆分为无限多个扇形,于是立刻得到圆面积公式:
S=πr·r=πr²
开普勒说小等腰三角形的面积等于对应的小扇形面积。如果把圆分为有限个扇形,那么两者不相等,误差是一个常量;而开普勒大胆地把圆分为无穷多个扇形,误差是一个变量,所以他才充满自信地断言两者相等。
开普勒的年代虽然对数诞生了,但是还没有微积分。他的公式推导还是非常精彩,答案也是正确的。
从有限到无穷,数学产生了飞跃式的发展。康托尔对无穷王国的征服,不仅回答了伽利略的疑问,还谱写了数学史上的华彩乐章!
科学尚未普及,媒体还需努力。祝阅读愉快,再见。
