标题:数列的通项公式
王福荣(上海市洋泾中学)
一个数列的第n项aₙ和项数n之间的函数关系,如果可用一个公式来表示,这个公式就叫做这个数列的通项公式。知道了数列的通项公式,就可写出该数列的任意项;还可用来研究数列的性质。因而,掌握数列通项公式的求法,是学习数列的重点之一。
大家知道,对于等差数列和等比数列,通项公式可通过首项a,公差d,公比q,及项数n来表示,即有
等差数列的通项公式是:
aₙ=a+(n-1)d,
等比数列的通项公式是:
aₙ=aqⁿ⁻¹.
对于任何数列,如果知道了前n项之和Sₙ的表达式,由于
Sₙ=a₁+a₂+···+aₙ₋₁+aₙ,故通项公式可用该数列的前n项之和与前n-1项之和的差来表示,即
aₙ=Sₙ-Sₙ₋₁
例如,已知数列{aₙ}的前n项之和为Sₙ=2n²-n,那么它的通项公式是:
aₙ=Sₙ-Sₙ₋₁
=(2n²-n)-[2(n-1)²-(n-1)]
=4n-3.
在通常的情况下,往往是给出数列的前几项,要求该数列的通项公式。这时,需要仔细观察每一项的结构,找出这些项的共同之处,发现它随着项数的变化而变化的规律。
[例1]求数列:

的通项公式。
解 这数列的每一项由两个分数的积构成,其中一个因数的分母是3的乘方形式,第n项就是3ⁿ;另一个因数分母是两个连续奇数的乘积,第n项是
(2n-1)(2n+1),故其通项公式是

[例2]求数列:

的通项公式。
解 上面这几项的共同特点是:每一项分子上的被开方数,比分母上的数大2。因而,若能找出分母随项数变化的规律,通项公式就能写出。数列前四项的分母是3,8,15,24, 它随着n的增大而增大,既非等差,又非等比,但不难发现它们与平方数4,9,16,25相差都是1,即8=3²-1,15=4²-1,24=5²-1,因而第n项的分母是(n+1)²-1;从而分子是

故通项公式是:

[例3] 求数列:8,88,888,8888,...的通项公式。
解 这个数列的特点是:各项中的数字都是8,且8的个数随着项数的增加而逐个增加。我们知道9=10-1,99=10²-1,...,
99...9(n个)=10ⁿ-1。故首先把原数列改写成各项都是由9表示的形式:

从而得其通项公式为:

有些数列,虽不具备该例的特点,但经过适当分解和组合,也能利用上面结果。
例如数列:35,3375,333775,33337775,...。这个数列各项中,3和7的个数随着项数的增加而逐个增加,且第n项是一个2n位数,即

为了能应用上例的结果,我们把它改写成:

[例4]已知a₁=1,a₂=2+3+4,a₃=5+6+7+8+9,a₄=10+11+12+13+14+15+16,...,求数列{aₙ}的通项公式。
解 这个数列的第n项是连续的2n-1个数之和,因而,如果能知道其第一个数,通项便能写出。因为1至n-1项,共有1+3+5+...+(2n-3)=(n-1)²个数,故第n项的第一个数是(n-1)²+1,所以通项是:

[例5]求数列:0,1,0,1,0,1,...的通项公式。
解 这个数列轮流地取0和1,呈周期性变化,我们不妨称它为周期数列。由于它的奇数项为0,偶数项为1,故通项为:
aₙ=½+(-1)ⁿ·½=½[1+(-1)ⁿ].
一般地,数列0,α,0,α,0,α,0,α,...
的通项为:
aₙ=½α[1+(-1)ⁿ];
数列β,0,β,0,β,0,β,0,...的通项为:
aₙ=½β[1+(-1)ⁿ⁺¹].
利用这个结果,我们来考察周期数列:
{aₙ}: 6,7,6,7,6,7,...
这个数列的任一项可看作如下两个数列:
{bₙ}: 6,0,6,0,6,0,...、
{cₙ}: 0,7,0,7,0,7,...
对应项之和,即
{aₙ}={bₙ}+{cₙ}。而
bₙ=3[1+(-1)ⁿ⁺¹],
cₙ=7/2[1+(-1)ⁿ],

从上面几例可以看出,除了一些特殊类型的数列(如等差数列,等比数列,周期数列)外,由于给出数列前几项的任意性,如由数列的前几项来确定通项,一般地说,无定法可循。
由数列的前几项来确定数列的通项,还需注意:
1.通项公式不是唯一的。
譬如在例2中,我们也可讲它的通项是

因为用n=1,2,3,4代入,它正好是
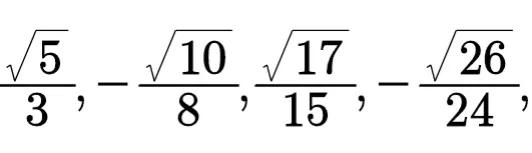
然而,这个通项公式不具有前几项所显示出来的规律,也较复杂。因此,实际上我们要求的通项公式,总是假定组成数列前几项的规律始终不变,而且是指很自然,或简单的通项公式。
2. 不是给出了一个数列的前几项,都可以写出其通项公式的。
譬如,所有质数,从小到大可排成一个数列:
2,3,5,7,11,13,17,19,...。
对此,我们无法写出其通项公式。
作为练习,请读者试写出下面各数列的通项公式:

科学尚未普及,媒体还需努力。感谢阅读,再见。龙年大吉
文章来源:
《数理化生园地》(上海科学技术出版社)1983第2辑
