被严重低估的王炸公式

题目呈现：直角三角形中的一个锐角为β，面积是12，(1)求此三角形的外接圆的面积；

(2)当β取何值时，外接圆的面积为最小？

要解答本题，需要用到三角公式。正弦和角公式的证明方法很多，在解题之前先介绍一个最简单的证明。这个证明出自张景中先生的数学科普著作。

把一个任意形状的普通三角形，作底边上的高，一分为二就得到两个直角三角形。读了张景中先生的书，知道从三角形面积等于两个直角三角形面积之和这个平凡的事实出发，就可以用三角形正弦面积公式推导出非常重要的正弦和角公式：sin(α+β)=sinαcosβ+cosαsinβ

如图所示，在三角形ABC中，角A可能是锐角、直角或钝角，而角α和角β都是锐角。BC是底边，D是垂足。AB=c，AC=b，AD=h。

用三角形正弦面积公式可以列出面积方程：

去分母，用2乘以方程两边，得

bcsin(α+β)=chsinα+bhsinβ

用bc除以方程两边，得

根据正弦函数的概念可得

因为sin B=sin(90°-α)=h:c

及sin C=sin(90°-β)=h:b

所以有

sin(α+β)=sinα·sin(90°-β)+sin(90°-α)·sinβ

又sin(90°-α)=cosα，sin(90°-β)=cosβ

所以有

sin(α+β)=sinαcosβ+cosαsinβ

课本上的正弦两角和与差公式：

sin(α±β)=sinαcosβ±cosαsinβ.

记忆方法：

异名积，符号同

口诀：sccs（函数名）

这个简单的证明充分发挥了面积法的威力，让人印象深刻。

以和角公式为基础，我们可以容易地推导出二倍角公式：

sin 2α

=sin(α+α)

=sin α∙cos α+cos α∙sin α

=2sin α∙cosα

准备工作顺利完成，现在可以开始解题了。

请大家思考一下，怎样解答本题：

直角三角形中的一个锐角为β，面积是12，(1)求此三角形的外接圆的面积；

(2)当β取何值时，外接圆的面积为最小？

几张图片后揭晓答案。

喝开水就能思路秒开，灵感迸开，能量炸开，美颜已开？

相信的人说心诚则灵，即信则有，不信则无。所以有考神保佑的挂件出售。

那么有没有火力全开，笑逐颜开，花儿盛开，桃花朵朵开？

闲话少叙，现在开始解题：

如图所示，设直角三角形的斜边为2r，则AC=2rsinβ，BC=2rcosβ，故

½(2r· cos β·2rsinβ)=12

∴r²sin2β=12

即

若⊙O为其外接圆，则其半径为r。

(1)外接圆面积

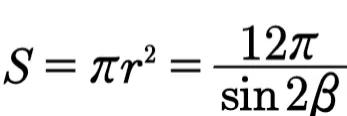
(2)当sin2β取最大值1，即2β=½π，β=¼π时，外接圆面积最小。

题目做完后再次回顾，又有新的感悟。本题第二问问的是当β取何值时，外接圆的面积为最小？因为斜边是直角三角形外接圆直径，所以这相当于是在问一个直角三角形面积为常数时，锐角β取何值斜边最短？

请看下图：

比较两个直角三角形(直径所对的圆周角均为直角)，它们斜边相等，高不相等，故面积不相等。若要直角三角形ABC的两个锐角角度不变，增加面积与直角三角形ABD相等，必然要延长斜边。所以可以直观地得到一个结论：面积一定的直角三角形中，斜边最短的必然是等腰直角三角形。同理可证，斜边一定的直角三角形中，等腰直角三角形面积最大。

继续追问，当三角形面积一定时，什么形状的三角形外接圆面积最小？

由以上推理可知，当三角形面积为定值时，要让外接圆半径R取最小值，那么abc就必然取最大值。所以，等边三角形的外接圆半径最小。

换句话说，当三角形的周长一定时，等边三角形面积最大。熟悉等周问题的读者都知道这个结论。