【兰利不定角度问题】

你注意到“这条辅助线”了吗？

"非典型问题"是什么样的问题

兰利问题(求角α的角度)

玛丽：想要具备数学能力，认真做题很重要。

马苏：只要你的目标不是高门槛的学校，一边学习①类问题，一边拓宽自己所掌握的知识来解决②类问题就可以了。

玛丽：如果没有数学天赋，还是很难的吧？

马苏：要扩展知识点，确实需要应用能力。不过，这是知识的延伸，所以你可以通过努力来实现。真正需要数学天赋的问题，其难度与②类问题不同。

玛丽：欸……那是什么问题呢？

马苏：比如下面这样的问题。

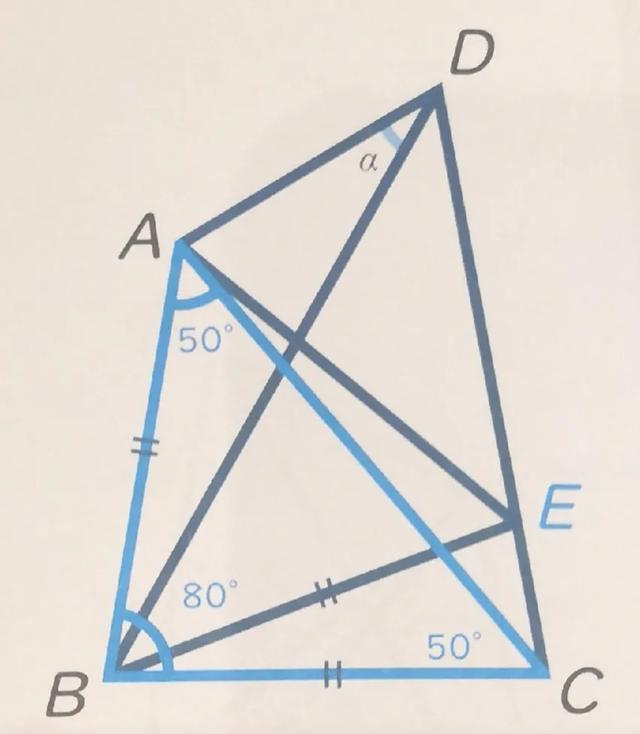
问题：在图中，求出∠α的大小。

玛丽：嗯？上图既不是平行四边形也不是梯形，是普通的四边形吧？

马苏：是的。所以，不能使用平行线的内错角和三角形的全等来解决。

玛丽：四边形中三角形角度的信息也不充分，仅靠这些是不可能得出答案的。

马苏：这是一个被称为"兰利问题"的著名问题，如果画上平时想不到的辅助线，你会发现答案是30°。

首先，在 CD 上取一个点 E ，使 ∠EBC =20°，如下页图所示。

图二

玛丽：是吗？为什么要在这么奇怪的地方取点 E 呢？

马苏：这就是所谓的"天才的灵感"吧。虽然看起来很奇怪，但很有效。下一步，画出辅助线 AE 和 BE。 则， BC = BE 。

玛丽：这是为什么呢？

马苏：首先，∠BCA =50°、 ∠ECA =30°，所以，∠BCE =80°。在三角形 BCE 中，∠ CBE + ∠BCE =100°。

由于三角形的内角和为180°，所以，∠BEC =80°。

玛丽：也就是说，三角形 BCE 有两个内角都是80°。

马苏：你注意到了。

换句话说，∠BCE=∠BEC =80°，所以，三角形 BCE 是等腰三角形，如下图所示。

图三

我们接着看三角形 ABC 。在三角形 ABC 中， ∠BCA =50°、 ∠ABC =80°，所以，由三角形的内角和可知， ∠BAC =50°。

玛丽：此时，∠BCA = ∠BAC =50°，所以，三角形 ABC 也是等腰三角形！

马苏：没错。

由此，可知 AB = BC ，根据以上证明， AB = BE ，如下页图所示。

图四

玛丽：嗯？因为三角形 ABC 是等腰三角形……

马苏：因为三角形 ABC 是等腰三角形， AB = BC ，三角形 BCE 也是等腰三角形，所以 BC = BE 。即 AB = BC = BE 。

玛丽：原来如此。

马苏：下面来看看三角形 ABE.

因为 AB = BE ，所以三角形 ABE 是等腰三角形。

并且，顶角∠ABE =60°，由此可知，三角形 ABE 是等边三角形。

玛丽：终于出现等边三角形了。

图五

马苏：现在看一下三角形BCD.由上图可知，∠BDC=180°-(60°+80°)=40°。由此，∠EBD=∠EDB=40°，BE=DE，所以三角形BDE是等腰三角形。

如果把相等的边整理出来，会发现AB=AE=BE=DE=BC

玛丽：这道题的图形相当特殊啊！

马苏：在这当中，请注意AE=DE,∠BEC=80°,∠BEA=60°.平角=180°，所以∠AED=40°，并且AE=DE,所以三角形EAD是顶角为40°的等腰三角形的底角。

玛丽：哇！这么说来就可以知道其它两个角的大小了。

图六

马苏：嗯。在上图中，∠ADE是顶角为40°的等腰三角形的底角，另外，等腰三角形的底角相等，所以

(180°-40°)÷2=70°

也就是说，∠ADC=70°

玛丽：大部分角度都知道了！接下来还需要知道什么呢？

马苏：现在终于可以求顶部的∠α了。如下图所示：

∠α的角度等于∠ADC减去∠BDC。已知∠BDC=40°，

∠α=∠ADC-∠BDC=70°-40°=30°

"非典型问题"不会也没办法

马苏：这个问题果然很棘手！

玛丽：这太难了……一会儿我还要再看4遍左右（汗）。

马苏：这个过程确实非常复杂。

但是，请冷静下来再看一看，基本上是简单的数学知识就能解决的问题吧？

玛丽：这么说来，确实如此！

所用的知识点，只有等腰三角形和等边三角形等事实。

马苏：这个问题之所以很难，是因为在几乎没有任何提示的情况下，需要"找出点 E ，并作出两条辅助线"。

玛丽：在所有的选择中，选中点 E 的理由几乎是事后才知道的。

马苏：没错。对于普通人来说，在画辅助线的阶段，还不知道能否推导出答案。

玛丽：虽说是"谜之线"，但只要继续下去，答案就能一点一点推导出来。

马苏：像这样的"谜之线"，如果没有数学天赋，是很难想到的。

玛丽：除非和马苏老师一样优秀，否则都会觉得很难吧……

马苏：不，我第一次碰到也是答不出来的。

我是因为本身就喜欢关于图形的问题，在中学的时候又遇到了兰利问题。我总在想："为什么要画那样的辅助线呢？"顺便说一下，兰利问题可以通过改变问题陈述中角度的数值，来产生各种各样的问题。这次，我选择了其中解法较短的题目。

玛丽：那个世界真了不起啊。

马苏：虽说如此，如果不是特殊情况，这类问题也不会出现。

因为高考的目的是检验"高中数学水平能力"，而不是"天才的灵感能力"。

玛丽：也就是说，在这些问题上不需要太努力吗？

马苏：是的。

③类问题主要是以奥林匹克数学为主的问题。一般来说，我认为用①类中频繁出现的问题和②类中应用的问题来培养自己的实力比较好。

你没必要因为无法解决像③类那种需要想象力的问题而感到沮丧。

玛丽的笔记

·有一些难题，如兰利问题，是无法通过背诵典型问题＋应用能力来解决的。

·有些难题只有少数天才能解决，所以即使不能解决也没必要沮丧。

以上内容摘自日本数学家的著作《授人以渔的数学法则教科书》第三章“通过努力能解决的问题"和"需要天赋才可以解决的问题”。

本书作者是网站“高中数学的美好故事”的站长，在网站使用笔名马苏。

兰利问题由英国数学家兰利提出，已经有超过一百年的历史了。

除了本文的解法，还可以用三角函数法求解。最能够让人大彻大悟醍醐灌顶的解法是汤普森的18等分圆的方法。

连接圆的两个相邻的18等分点和圆心，就得到一个顶角为20°，两个底角为80°的等腰三角形。以此为基础，就可以构造出兰利的四边形(四边形ABMN)。

兰利问题考察的是数学方面的想象力和创造力，是需要天赋才能解决的问题。