蒋声（扬州师范学院数学系副教授）

设在平面上已知定点 P 和定圆 O ．过 P 任作一条与圆 O 相交的直线，设交点为 A 和 B ．当这条直线绕点 P 旋转时，线段 PA 和 PB 的长度都在改变，但由切割线定理和相交弦定理可知，乘积 PA · PB 却保持定值。这个定值可以用定点到圆心的距离 PO 和圆半径 r 表示出来。当点 P 在圆外时（图1)，设 PT 为圆的切线，则

PA·PB =PT²=PO²-r²;

而当 P 在圆内时（图2)，设 MN 是过 P 的直径，则

PA·PB=PM·PN=(r+PO)(r-PO)=r²-PO².

图2

图1

现在用 PA 和 PB 表示有向线段，那么，当 P 在圆外时， PA 与 PB 同向，其乘积为正（等于 PA · PB )；而当 P 在圆内时， PA 与 PB 反向，其乘积为负（等于- PA·PB )。从上述讨论可知，在这两种情形下，都有

PA · PB =PO²-r²

又，若P在圆周上，则P与一个交点B重合，因而PB=0，仍有 PA·PB =0=PO²-r².

总之，在每种情形下， PA · PB 都是一个常数 k ，并且等于 PO²-r²。这个常数k叫做点 P 关于圆 O 的幂，简称圆幂。当 P 在圆外时，圆幂 k >0; P 在圆内时， k <0; P 在圆周上时， k =0.切割线定理和相交弦定理统称圆幂定理。

圆幂定理在解题中非常有用，下面通过例题介绍几种常见的应用方式。

［例1]在圆 O 中，已知弦 AB = b ，弓形 ANB 的高为 h ,求圆的直径 d .

解 如图3，作垂直于 AB 的直径 MN ，垂足为 P ．由相交弦定理，得

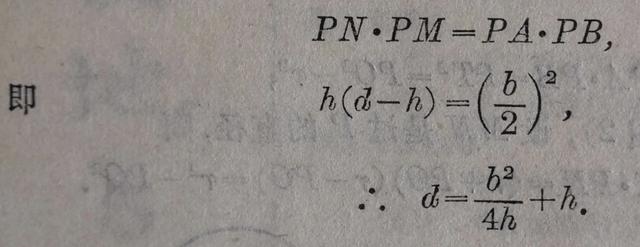
PN · PM = PA · PB ,

即 h ( d - h )=(b/2)²,

图3

例1是一个富有实用价值的计算题。在生产中，常需根据破碎的砂轮或其他圆形零件的残片配换新零件，这时可用游标卡尺测出 b 和 h ，代入例1所得的公式，就可算出圆直径 d ．利用圆幂定理，还可解一些有关圆的其他计算题。

［例2] PN 是圆 O 的切线，切点为 N 。取 PN 的中点 M ，过 P 、 M 任意作圆O₁，交圆 O 于 A 、 B ，直线 AB 交 PN 于 Q ，则 MQ:QN:PM:PQ=1:2:3:4.

证明 如图4，记 PM = a , MQ = x ，则 MN = a , QN = a - x ．在圆O₁中，应用切割线定理，得

QM·QP = QA·QB ;

在圆 O 中，应用切割线定理，得

QA·QB =QN².

由此得到QM·QP=QN²,即x(a+x)=(a-x )²。化简后，利用 a ≠0，得到 a =3x，即

PM = MN =3MQ.

由此推出

QN =3MQ- MQ =2MQ,

PQ =3MQ+ MQ =4MQ.

∴MQ : QN : PM : PQ =1:2:3:4.

例2表明，圆幂定理很适合于用来论证一些与圆有关的线段之间的比例关系和相等关系。

［例3]设 AB 是圆 O 的切线， B 是切点， M 是 AB 的中点．过 M 作割线交圆于 C 、 D ，连 AC 、 AD 又交圆于 E 、 F ，则 AB ∥ EF .

证明 如图5，由切割线定理得MB²= MC·MD ．而 MA = MB ，所以MA²= MC·MD ，即

由此推出△MCA∽△MAD ，所以∠MAC =∠MDA ．从圆 O 又得到∠MDA =∠CEF ，所以∠MAC=∠CEF ，由此得到 AB // EF .

例3表明，把圆幂定理与相似三角形结合起来，还能论证角的相等关系，因而可用来解决有关平行和垂直的问题。

借助相似三角形，容易证明圆幂定理的逆命题也是正确的。这些逆命题是：

1．若线段AB和CD交于点P ，使 PA·PB = PC·PD ，则 A 、 B 、 C 、 D 四点共圆；

2．若∠P 的两边上各有两点 A 、 B 和 C 、 D ，使 PA · PB = PC·PD ，则 A 、 B 、 C 、 D 四点共圆；

3．若∠P 的一边上有两点 A 、 B ，另一边上有点 T ，使 PA · PB =PT²，则△ ABT 的外接圆与 PT 相切．

这些逆命题使圆幂定理与四点共圆问题联系起来，因而扩大了应用范围，并且更便于用来研究角的相等、平行、垂直等问题．

［例4]设 PA 和 PB 是圆 O 的切线， A 、 B 是切点。过 AB 的中点 M 任意作弦 CD ，则∠ APC =∠BPD.

证明 如图6，因为 PA 和 PB 是圆 O 的切线，所以 PA⊥OA, PB⊥OB ，因而A和B都在以 OP 为直径的圆上，并且由对称性知 OP 过 AB 的中点 M ．由圆幂定理，得MP·MO=MA· MB 。从圆 O 又得到 MA·MB = MC·MD ，所以 MP·MO = MC·MD 。由圆幂定理的逆命题知 P 、C、 O 、 D 四点共圆，因而从OC= OD 得∠OP=∠OPD ．再注意 ∠OPA =∠OPB ，就得到∠ APC =∠BPD .

圆幂在圆的几何学中占有重要地位，圆的几何学与中学课本相距较远，这里就不介绍了。

文章来源：《数理化生园地》第五辑(1984/1)