哥德巴赫猜想，一句听起来简单到离谱的话：任何一个大于 2 的偶数，都可以写成两个质数之和。

比如 4=2+2，6=3+3，8=3+5，10=3+7，12=5+7…… 你随便找一个偶数来试，都能满足这个规律。就连小学生都能理解的命题，却让全世界最顶尖的数学家们头疼了近 300 年。

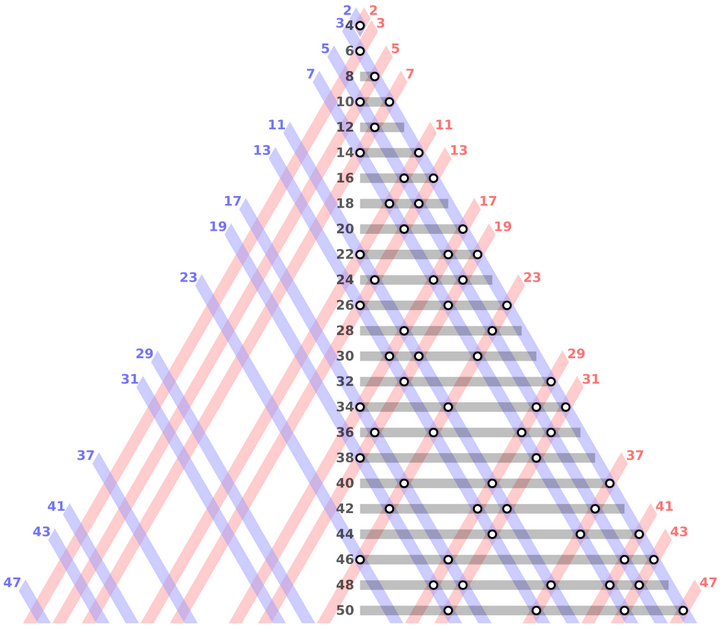
从 1742 年哥德巴赫在给欧拉的信中提出这个猜想，到现在已经过去 280 多年。期间，无数数学家前赴后继，却始终没能彻底攻克。最接近的成果是 1966 年陈景润证明的 “1+2”—— 任何一个充分大的偶数，都可以写成一个质数与两个质数乘积之和。但这距离最终的 “1+1”，还差关键的一步。

这就很让人困惑了：一个连小学生都能看懂的猜想，为什么证明起来会这么难？它到底难在哪里？更重要的是，花了近 300 年时间去证明一个看似 “没用” 的猜想，到底值不值得？它对数学发展到底有什么实际推动作用？

哥德巴赫猜想到底在说什么？

很多人可能只知道 “1+1=2” 的通俗说法，但其实哥德巴赫猜想有两个部分，而且最初的表述和现在我们熟知的版本还有些区别。

猜想的两个部分：奇数和偶数

1742 年，普鲁士数学家克里斯蒂安・哥德巴赫在给瑞士数学家莱昂哈德・欧拉的信中，提出了两个猜想：

第一部分（奇数猜想）：任何一个大于 5 的奇数，都可以写成三个质数之和；

第二部分（偶数猜想）：任何一个大于 2 的偶数，都可以写成两个质数之和。

这两个猜想是相互关联的。欧拉在回信中表示，他虽然不能证明这两个猜想，但他相信它们都是正确的。而且，欧拉指出，如果第二部分（偶数猜想）能够被证明，那么第一部分（奇数猜想）就可以很容易推导出来。

比如，假设偶数猜想成立，那么对于任何一个大于 5 的奇数 N，N-3 就是一个大于 2 的偶数，根据偶数猜想，N-3 可以写成两个质数之和（比如 p+q），那么 N=3+p+q，也就是三个质数之和，奇数猜想就成立了。

正因为如此，后来的数学家们把主要精力都放在了偶数猜想的证明上。我们现在所说的 “哥德巴赫猜想”，通常指的就是这个偶数猜想 —— 任何一个大于 2 的偶数，都可以表示为两个质数之和，也就是俗称的 “1+1”（1 个质数 + 1 个质数）。

无规律才是最大的规律

要理解哥德巴赫猜想的难度，首先得明白质数的特性。质数是指大于 1 的自然数中，除了 1 和它本身以外，没有其他因数的数（比如 2、3、5、7、11、13 等）。

质数的最大特点就是：没有统一的分布规律。虽然随着自然数的增大，质数的个数会逐渐减少（比如 1 到 100 中有 25 个质数，1 到 1000 中有 168 个质数，1 到 10000 中有 1229 个质数），但它们在自然数中的分布是随机的、无规律的。我们无法用一个公式来预测下一个质数是什么，也无法确定两个相邻质数之间的间隔有多大（间隔可以是 2，也可以是几十、几百甚至更大）。

这种 “无规律性”，正是哥德巴赫猜想难以证明的核心原因之一。因为要证明 “任何大于 2 的偶数都能写成两个质数之和”，本质上是要证明 “对于任意一个偶数 N，在小于 N 的质数中，一定存在两个质数 p 和 q，使得 p+q=N”。但由于质数的分布没有规律，我们无法直接构建这样的 p 和 q，也无法用常规的数学方法去遍历所有偶数，只能通过间接的、迂回的方式去逼近结论。

举个例子，我们可以验证 100 以内的所有偶数都满足哥德巴赫猜想，也可以用计算机验证 1000 万、100 亿甚至更大的偶数都满足，但 “验证” 不等于 “证明”。数学证明需要保证 “对于所有大于 2 的偶数，无一例外都满足”，而不是 “我们验证过的偶数都满足”。这就像我们永远无法通过数羊来证明 “所有羊都是白色的”—— 哪怕你数了 100 万只白色的羊，只要出现一只黑色的羊，这个结论就不成立。

哥德巴赫猜想的证明，就是要找到一种方法，确保 “黑色的羊” 永远不会出现，而这种方法，必须突破质数无规律分布带来的障碍。

从 “验证” 到 “证明”

很多人可能会觉得，既然我们已经用计算机验证了极其庞大的偶数都满足哥德巴赫猜想，为什么还需要费力去证明？这就涉及到数学的核心特质 —— 严谨性。

数学不是实验科学，它不依赖于 “多次验证正确” 就得出结论。比如，曾经有数学家提出 “对于所有自然数 n，n²-n+41 都是质数”，这个式子在 n=1 到 40 时都成立（1²-1+41=41 是质数，2²-2+41=43 是质数……40²-40+41=1601 是质数），但当 n=41 时，41²-41+41=41²=1681=41×41，不是质数，这个猜想就被推翻了。

再比如，“费马大定理”（xⁿ+yⁿ=zⁿ，当 n>2 时没有正整数解），费马在 17 世纪提出这个猜想后，数学家们验证了 n=3、4、5…… 直到很大的数都没有找到解，但直到 1994 年，安德鲁・怀尔斯才最终证明了这个定理，历时 350 多年。

哥德巴赫猜想也是如此。哪怕我们验证了 10¹⁸（10 的 18 次方）以内的所有偶数都满足猜想，也不能保证 10¹⁸+2 这个偶数一定能写成两个质数之和。数学需要的是绝对的、普遍的成立，而不是有限范围内的验证。

哥德巴赫猜想的难点一

正如我们之前所说，质数的分布是无规律的，这是哥德巴赫猜想最根本的难点。

在数论中，描述质数分布的核心定理是 “质数定理”：不大于 n 的质数的个数 π(n)，大约等于 n/lnn（ln本身是“自然对数” 的符号，lnn是变量n的自然对数）。这个定理虽然揭示了质数个数随 n 增长的大致趋势，但它只是一个 “渐近公式”，无法精确描述每个质数的具体位置，也无法告诉我们在某个区间内有多少个质数，更无法直接关联到 “两个质数之和等于某个偶数”。

比如，对于一个很大的偶数 N，我们知道在 1 到 N 之间有大约 N/lnN 个质数，但我们不知道这些质数中是否一定有两个质数的和等于 N。质数定理只能告诉我们 “质数很多”，但不能告诉我们 “这些质数中存在满足条件的一对”。

要证明哥德巴赫猜想，就需要找到一种方法，将质数的分布与偶数的分解联系起来。但由于质数分布没有简单的公式，这种联系很难建立。数学家们只能通过间接的方式，比如估计在某个区间内质数的个数、研究质数的密度、分析质数的算术级数分布等，来逼近这个目标，但每一步都异常艰难。

哥德巴赫猜想的难点二

哥德巴赫猜想是一个 “存在性命题”—— 对于任意大于 2 的偶数 N，存在两个质数 p 和 q，使得 p+q=N。

在数学中，存在性命题的证明通常有两种思路：一种是 “构造性证明”，即直接找到满足条件的 p 和 q，或者给出找到它们的通用方法；另一种是 “非构造性证明”，即通过逻辑推理证明这样的 p 和 q 一定存在，而不需要具体找到它们。

但对于哥德巴赫猜想来说，这两种思路都面临巨大的挑战：

构造性证明：由于质数分布无规律，我们无法给出一个通用方法，对于任意偶数 N，都能快速找到满足 p+q=N 的质数 p 和 q。虽然对于具体的偶数，我们可以通过计算机搜索找到这样的质数，但这不能推广到所有偶数；

非构造性证明：要证明 “存在”，就需要找到一个合适的数学工具，将 “偶数 N” 与 “两个质数之和” 联系起来。但数论中缺乏直接描述这种联系的理论，数学家们只能借助分析、代数、组合等多个分支的工具，间接证明存在性，但这些工具的结合本身就是一个巨大的难题。

更关键的是，哥德巴赫猜想要求 “对于所有偶数 N” 都成立，这意味着存在性证明必须是普遍的、无例外的。而很多非构造性证明只能证明 “存在无穷多个偶数满足条件”，或者 “几乎所有偶数满足条件”，但无法证明 “所有偶数都满足条件”—— 这正是哥德巴赫猜想的核心要求。

哥德巴赫猜想的难点三

在哥德巴赫猜想提出后的很长一段时间里，数学家们都只能用初等数论的方法去尝试证明，但始终没有进展。这是因为初等数论的工具（比如整除、同余、质数定理的初等形式等）对于处理 “质数分布的存在性” 问题，显得力不从心。

直到 20 世纪初，数学家们才意识到，要证明哥德巴赫猜想，必须引入新的数学工具，比如分析数论中的圆法、筛法等。这些工具的引入，虽然让证明有了突破（比如陈景润的 “1+2”），但也带来了新的问题：这些工具本身存在局限性，无法直接推向 “1+1”。

圆法：看似可行，却卡在 “奇点” 上

圆法是由英国数学家哈代和李特尔伍德在 1920 年代提出的，它的核心思想是将数论问题转化为复分析中的积分问题。具体来说，就是通过构造一个积分，将 “偶数 N 可以表示为两个质数之和的个数” 与这个积分的结果联系起来。如果能证明这个积分的结果对于所有大于 2 的偶数 N 都大于 0，那么哥德巴赫猜想就成立。

圆法的提出，让哥德巴赫猜想的证明有了明确的方向。哈代和李特尔伍德甚至用圆法证明了 “在广义黎曼猜想成立的前提下，每个充分大的奇数都可以表示为三个质数之和”（即哥德巴赫猜想的奇数部分）。但对于偶数部分，圆法遇到了一个致命的问题：积分中存在 “奇点”（即积分发散的点），这些奇点来自于质数的分布特性，无法用常规的复分析方法处理。

要解决奇点问题，就需要对质数的分布有更精确的了解，而这正是目前数学界还没有攻克的难题。虽然后来的数学家们对圆法进行了改进，但始终无法彻底解决奇点带来的困扰，这也使得圆法无法直接证明 “1+1”。

筛法：逼近 “1+1”

筛法是另一种重要的工具，它的起源可以追溯到古希腊数学家埃拉托斯特尼的 “素数筛”—— 通过筛选掉合数，留下质数。20 世纪以来，数学家们对筛法进行了多次改进，使其成为证明哥德巴赫猜想的主要工具之一。

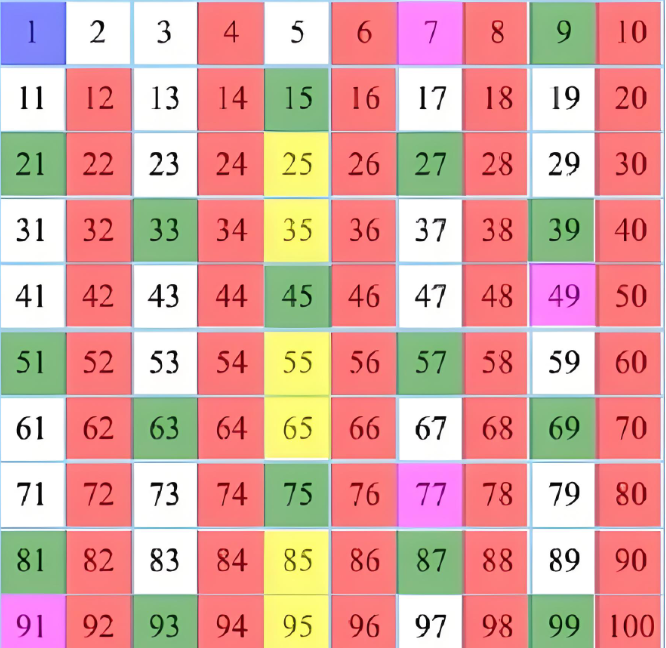
筛法的核心思想是：对于一个偶数 N，要证明存在两个质数 p 和 q 使得 p+q=N，就相当于证明在 1 到 N-1 的质数中，存在一个质数 p，使得 N-p 也是质数。筛法通过构造一个 “筛函数”，来估计满足条件的质数 p 的个数。如果能证明这个个数大于 0，那么哥德巴赫猜想就成立。

从筛法的发展来看，数学家们一步步逼近了 “1+1”：

1920 年，挪威数学家布朗证明了 “9+9”（任何一个充分大的偶数，都可以表示为两个至多 9 个质因数的乘积之和）；

1924 年，德国数学家拉德马赫证明了 “7+7”；

1932 年，英国数学家埃斯特曼证明了 “6+6”；

1937 年，意大利数学家蕾西证明了 “5+7”“4+9”“3+15”“2+366”；

1938 年，苏联数学家布赫夕太勃证明了 “5+5”；

1940 年，布赫夕太勃又证明了 “4+4”；

1956 年，中国数学家王元证明了 “3+4”，随后又证明了 “3+3”“2+3”；

1962 年，中国数学家潘承洞证明了 “1+5”，王元、潘承洞合作证明了 “1+4”；

1965 年，苏联数学家维诺格拉多夫和意大利数学家朋比利证明了 “1+3”；

1966 年，中国数学家陈景润证明了 “1+2”。

从 “9+9” 到 “1+2”，筛法取得了巨大的进展，但为什么始终无法跨越到 “1+1”？这是因为筛法本身存在局限性：

筛法的本质是 “筛选”，它通过排除合数来保留质数，但在筛选过程中，会不可避免地 “误伤” 一些质数，或者无法精确区分质数和 “几乎质数”（即质因数个数很少的合数）。要证明 “1+1”，需要筛法能够精确地筛选出 “p 是质数且 N-p 是质数” 的情况，但目前的筛法工具无法做到这一点 —— 当筛法试图将质因数个数减少到 1 时，筛选的精度会急剧下降，无法保证结果的准确性。

并且，哥德巴赫猜想不是一个孤立的问题，它与数论中的其他多个难题（比如黎曼猜想、孪生素数猜想、弱哥德巴赫猜想等）有着深度关联。这些难题相互交织，形成了一个复杂的 “问题网络”，要证明哥德巴赫猜想，可能需要先解决其他难题，或者需要找到一种能同时解决多个难题的全新思想。

哥德巴赫猜想的证明过程

第一阶段：1742-1900 年，初等数论

哥德巴赫猜想提出后，欧拉虽然相信它是正确的，但始终没能给出证明。在接下来的 100 多年里，数学家们主要用初等数论的方法（比如整除、同余、不定方程等）去尝试证明，但都没有取得实质性进展。

这一阶段的数学家们，大多是通过验证具体的偶数来寻找规律，或者试图构造一些特殊的形式来证明猜想，但由于初等数论工具的局限性，始终无法突破 “所有偶数” 这一普遍条件。比如，法国数学家勒让德在 1808 年试图用初等方法证明哥德巴赫猜想，但最终只能证明一些特殊情况下的偶数满足条件，无法推广到所有偶数。

数学家们意识到，仅靠初等数论的方法，很难证明哥德巴赫猜想，必须寻找新的思路和工具。

第二阶段：1900-1950 年，分析数论

20 世纪初，随着分析数论的发展，数学家们开始将复分析、实分析等工具引入哥德巴赫猜想的研究，这才让证明有了实质性的突破。

哈代与李特尔伍德的圆法（1920 年代）

这个方法前面提到，1920 年，英国数学家哈代和李特尔伍德在《论哥德巴赫问题》一文中，提出了圆法。这是哥德巴赫猜想研究史上的一个里程碑式的贡献。

圆法的核心思想是将数论问题转化为复积分问题。具体来说，对于偶数 N，构造一个积分：

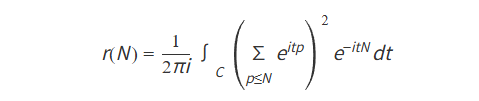
其中，C 是复平面上的一个圆周，p 是质数。r (N) 表示将偶数 N 表示为两个质数之和的个数。如果能证明对于所有大于 2 的偶数 N，r (N) > 0，那么哥德巴赫猜想就成立。

哈代和李特尔伍德用圆法证明了：在广义黎曼猜想成立的前提下，每个充分大的奇数都可以表示为三个质数之和（即奇数哥德巴赫猜想的弱化形式）。虽然他们没有证明偶数哥德巴赫猜想，但圆法的提出，为后续的研究提供了明确的方向。

布朗的筛法（1920 年）

1920 年，挪威数学家布朗对埃拉托斯特尼筛法进行了改进，提出了 “布朗筛法”。他用这种方法证明了 “9+9”—— 任何一个充分大的偶数，都可以表示为两个至多 9 个质因数的乘积之和。

布朗筛法的核心是 “加权筛法”，通过给每个数赋予一个权重，来更精确地估计满足条件的数的个数。虽然 “9+9” 离 “1+1” 还很远，但它首次证明了 “每个充分大的偶数都可以表示为两个‘几乎质数’之和”，为后续的研究打开了大门。

维诺格拉多夫的三角和方法（1937 年）

1937 年，苏联数学家维诺格拉多夫改进了圆法，提出了 “三角和方法”。他用这种方法，在不假设黎曼猜想成立的情况下，证明了 “每个充分大的奇数都可以表示为三个质数之和”。这一成果彻底解决了哥德巴赫猜想的奇数部分，让人们看到了圆法的巨大潜力。

维诺格拉多夫的证明，是分析数论在数论问题中的一次重大胜利。他通过对三角和的精确估计，克服了圆法中的奇点问题，为偶数哥德巴赫猜想的证明提供了重要的参考。

第三阶段：1950-1970 年， “1+2” 的诞生

这一阶段，数学家们的主要精力集中在改进筛法上，通过不断减少 “几乎质数” 的质因数个数，一步步逼近 “1+1”。

中国数学家的崛起

从 1950 年代开始，中国数学家在哥德巴赫猜想的研究中崭露头角，取得了一系列重要成果：

1956 年，王元证明了 “3+4”，这是中国数学家在哥德巴赫猜想研究中取得的第一个重要成果；

1957 年，王元又证明了 “3+3” 和 “2+3”，进一步缩小了质因数个数的范围；

1962 年，潘承洞证明了 “1+5”，王元、潘承洞合作证明了 “1+4”；

1965 年，维诺格拉多夫和朋比利证明了 “1+3”；

1966 年，陈景润在《科学通报》上发表了 “1+2” 的证明摘要，1973 年发表了详细证明。

陈景润的 “1+2” 证明，是筛法的巅峰之作。他改进了之前的筛法，提出了 “加权筛法” 和 “主项估计”“余项估计” 的新方法，成功证明了 “任何一个充分大的偶数，都可以表示为一个质数与两个质数乘积之和”。

陈景润的证明，距离哥德巴赫猜想的最终目标 “1+1”，只有一步之遥。但这一步，却成为了近 50 年来无数数学家难以跨越的鸿沟。

第四阶段：1970 年至今，停滞阶段

自陈景润证明 “1+2” 以来，哥德巴赫猜想的研究陷入了停滞。虽然数学家们尝试了各种方法，比如改进圆法、筛法，引入代数几何、组合数学等新工具，但始终没有取得实质性的进展。

这一阶段的研究，主要集中在以下几个方向：

改进筛法的精度，试图将 “1+2” 推向 “1+1”，但由于筛法本身的局限性，始终无法突破；

利用计算机技术，验证更大范围的偶数满足哥德巴赫猜想，目前已经验证到 10¹⁸以内的偶数都满足猜想。

值得一提的是，2013 年，张益唐证明了 “存在无穷多对相差小于 7000 万的质数”，这一成果虽然是关于孪生素数猜想的，但它对筛法的改进，为哥德巴赫猜想的研究提供了新的思路。随后，数学家们将 “7000 万” 逐步缩小到 “246”，但这仍然没有直接推动哥德巴赫猜想的证明。

近 50 年来的停滞，让很多数学家意识到，要证明 “1+1”，可能需要一种全新的数学思想，甚至可能需要建立一门新的数学分支。目前的数学工具，无论是圆法、筛法，还是其他方法，都还不足以攻克这个难题。

为什么 “1+1” 至今无法突破？

虽然陈景润的 “1+2” 已经过去了近 50 年，但 “1+1” 的证明仍然没有进展。那么，为什么 “1+1” 会如此难以突破？

正如我们之前所说，目前证明哥德巴赫猜想的主要工具是圆法和筛法，但这两种工具都存在本质的局限性：

圆法无法解决偶数哥德巴赫猜想中的奇点问题，这些奇点来自于质数的分布特性，需要对质数分布有更精确的描述，而目前的数学理论还无法做到这一点；

筛法无法精确区分质数和 “几乎质数”，当试图将质因数个数减少到 1 时，筛选的精度会急剧下降，无法保证结果的准确性。

很多数学家认为，仅靠改进现有的圆法和筛法，已经无法证明 “1+1”，必须寻找全新的数学思想和方法。

要证明 “1+1”，可能需要一种全新的数学思想，这种思想可能会颠覆我们目前对数论的理解，甚至可能需要建立一门新的数学分支。

比如，有些数学家猜测，哥德巴赫猜想的证明可能需要用到 “朗兰兹纲领” 的思想。朗兰兹纲领试图将数论、代数几何、表示论等多个数学分支统一起来。如果朗兰兹纲领能够被证明，那么可能会为哥德巴赫猜想的证明提供全新的思路和工具。

还有些数学家认为，哥德巴赫猜想的证明可能需要用到 “量子数学” 的思想。量子数学是一门新兴的数学分支，它将量子力学的思想和方法应用于数学研究，可能会为解决传统数学难题提供新的方法。

数学的发展是一个漫长而缓慢的过程，很多重大的数学难题都需要几百年甚至上千年的时间才能被解决。哥德巴赫猜想已经困扰了数学家们近 300 年，它的证明可能还需要更长的时间。