8（下）数学每日一道压轴题（22-30）
莫等闲周周
2025-02-26 15:44:34
📌【八下数学压轴题5大必考题型】90%学生卡在这类题！附破解模板👇
---
❶ **平行四边形综合题**（高频！）
🔥 **命题套路**：
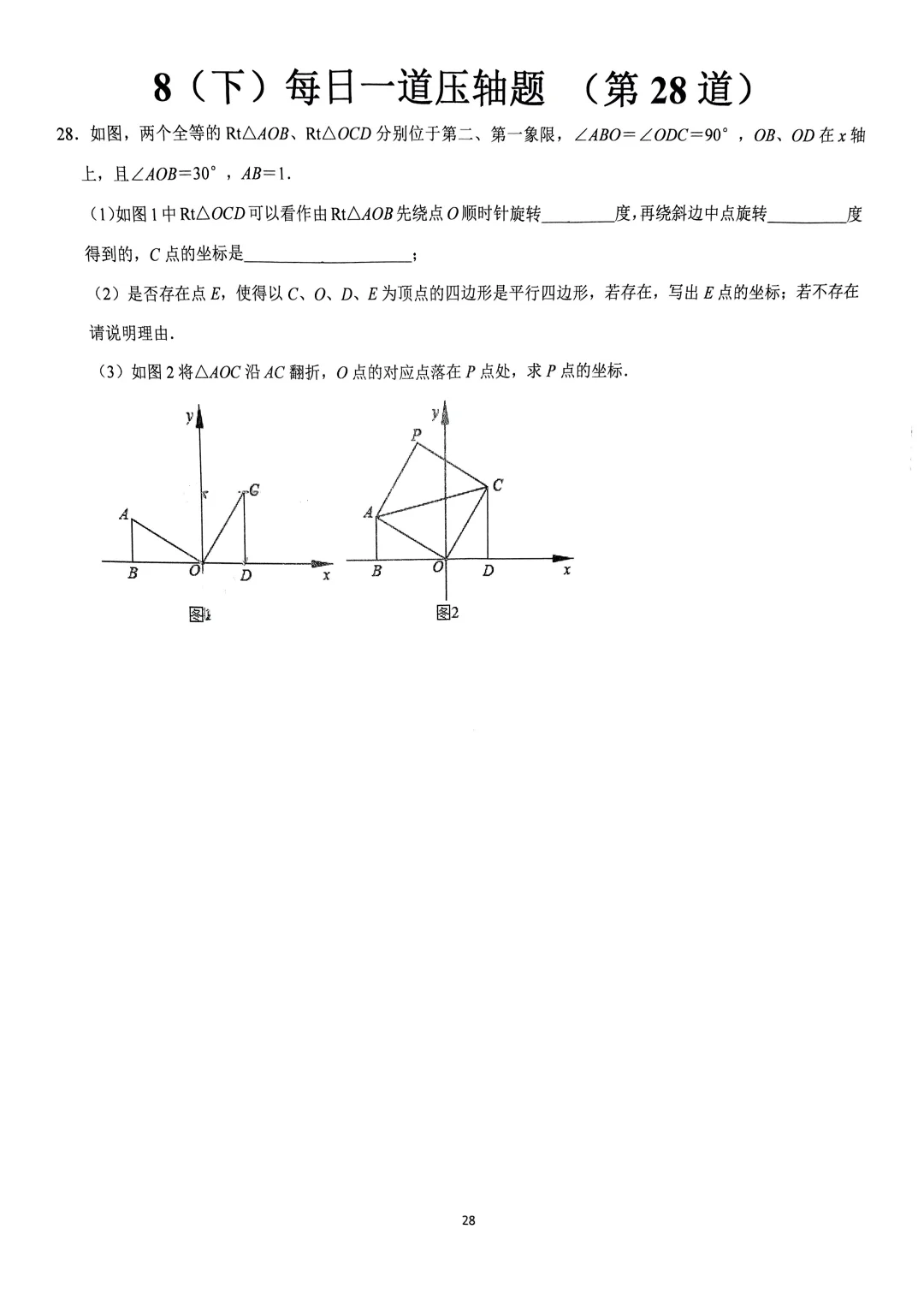
给折叠图形/坐标系中的四边形，要求证明菱形、矩形或存在性问题
✅ **解题模板**：
1. **判定定理法**：先证平行四边形（对边平行/对角相等）→再叠加特殊条件（邻边相等→菱形，有直角→矩形）
2. **坐标系必杀技**：用中点公式求对称点，勾股定理验证垂直
🌟 **例题特征**：常结合一次函数坐标点计算（如求D点使四边形ABCD为平行四边形）
---
❷ **一次函数与几何综合题**（易错！）
🚨 **经典考法**：
求两直线交点坐标→构造三角形面积最值→讨论点P是否存在使△为等腰/直角三角形
🔑 **破题关键**：
- **面积公式**：铅垂高×水平宽÷2（坐标系中快速求面积）
- **存在性问题**：设点坐标（如P(t,2t+3)）→用两点间距离公式列方程
⚠️ **必背模型**：等腰三角形用“两圆一垂直”，直角三角形用“勾股逆定理”
---
❸ **勾股定理折叠问题**（必考！）
📐 **解题步骤**：
1. 标折叠前后对应点（用△ABC→△A'B'C标记）
2. 设未知数表示边长（如设EC=x，则AE=8-x）
3. 在Rt△中列勾股方程（例：A'D² + DC² = A'C²）
💡 **速记口诀**：“折叠必全等，设x找直角，勾股解方程”
---
❹ **动点压轴题**（拉分关键！）
⏳ **三大类考法**：
- 四边形上的动点：求t值使四边形为菱形/梯形
- 函数图像上的动点：分段讨论面积与时间关系
- 双动点相遇问题：建立方程组解相遇时间
📝 **解题框架**：
1. 画运动过程分解图（0秒、t秒、临界点）
2. 用含t的代数式表示线段长（如AP=2t）
3. 分类讨论（通常有2-3种情况）
---
0
阅读：1
